
【題目】如圖,在三棱錐![]() 中,
中,![]() 為棱
為棱![]() 上的任意一點(diǎn),
上的任意一點(diǎn),![]() 分別為所在棱的中點(diǎn).
分別為所在棱的中點(diǎn).
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,當(dāng)二面角
,當(dāng)二面角![]() 的平面角為
的平面角為![]() 時,求棱
時,求棱![]() 的長.
的長.

【答案】(1)見解析;(2)2
【解析】分析:(1)要證BD//平面FGH,可先證平面ABP//平面FGH,而這由中位線定理易得線線平行,從而有線面平行,再得面面平行;
(2)可以C為原點(diǎn),CB為x軸,CP為z軸,建立如圖的空間直角坐標(biāo)系,設(shè)![]() ,寫出點(diǎn)的坐標(biāo),求得兩平面CGF和平面HGF的法向量,由法向量夾角與二面角的關(guān)系可求得
,寫出點(diǎn)的坐標(biāo),求得兩平面CGF和平面HGF的法向量,由法向量夾角與二面角的關(guān)系可求得![]() ,從而得PC的長.
,從而得PC的長.
詳解:(1)證明:因?yàn)?/span>![]() 分別為
分別為![]() 的中點(diǎn),
的中點(diǎn),
所以![]() ,且
,且![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因?yàn)?/span>![]() 分別為
分別為![]() 的中點(diǎn),所以有
的中點(diǎn),所以有![]() ,
,![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因?yàn)?/span>![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
因?yàn)?/span>![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 作
作![]() ,如圖所示,以
,如圖所示,以![]() 為原點(diǎn),
為原點(diǎn),![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標(biāo)系
軸建立空間直角坐標(biāo)系![]() .
.

由![]() 為等腰直角三角形知
為等腰直角三角形知![]() ,又
,又![]() ,
,![]() ,所以有
,所以有![]() 平面
平面![]() .
.
設(shè)![]() ,則
,則![]() ,
,![]() ,
,
所以![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
設(shè)![]() 為平面
為平面![]() 的一個法向量,則有
的一個法向量,則有 ,
,
即有![]() ,所以可取
,所以可取![]() .
.
由![]() ,得
,得![]() ,從而
,從而![]() .
.
所以棱![]() 的長為2.
的長為2.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列五個命題:
①函數(shù)f(x)=2a2x-1-1的圖象過定點(diǎn)(![]() ,-1);
,-1);
②已知函數(shù)f(x)是定義在R上的奇函數(shù),當(dāng)x≥0時,f(x)=x(x+1),若f(a)=-2則實(shí)數(shù)a=-1或2.
③若loga![]() >1,則a的取值范圍是(
>1,則a的取值范圍是(![]() ,1);
,1);
④若對于任意x∈R都f(x)=f(4-x)成立,則f(x)圖象關(guān)于直線x=2對稱;
⑤對于函數(shù)f(x)=lnx,其定義域內(nèi)任意x1≠x2都滿足f(![]() )≥
)≥![]()
其中所有正確命題的序號是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法中錯誤的個數(shù)是( )
①若直線![]() 平面
平面![]() ,直線
,直線![]() ,則
,則![]() ;②若直線l和平面
;②若直線l和平面![]() 內(nèi)的無數(shù)條直線垂直,則直線l與平面
內(nèi)的無數(shù)條直線垂直,則直線l與平面![]() 必相交;③過平面
必相交;③過平面![]() 外一點(diǎn)有且只有一條直線和平面
外一點(diǎn)有且只有一條直線和平面![]() 垂直;④過直線
垂直;④過直線![]() 外一點(diǎn)有且只有一個平面和直線a垂直
外一點(diǎn)有且只有一個平面和直線a垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年2月22日.在平昌冬奧會短道速滑男子500米比賽中.中國選手武大靖以連續(xù)打破世界紀(jì)錄的優(yōu)異表現(xiàn),為中國代表隊(duì)奪得了本屆冬奧會的首枚金牌,也創(chuàng)造中國男子冰上競速項(xiàng)目在冬奧會金牌零的突破.某高校為調(diào)查該校學(xué)生在冬奧會期間累計(jì)觀看冬奧會的時間情況.收集了200位男生、100位女生累計(jì)觀看冬奧會時間的樣本數(shù)據(jù)(單位:小時).又在100位女生中隨機(jī)抽取20個人.已知這20位女生的數(shù)據(jù)莖葉圖如圖所示.
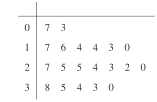
(1)將這20位女生的時間數(shù)據(jù)分成8組,分組區(qū)間分別為![]() ,在答題卡上完成頻率分布直方圖;
,在答題卡上完成頻率分布直方圖;
(2)以(1)中的頻率作為概率,求1名女生觀看冬奧會時間不少于30小時的概率;
(3)以(1)中的頻率估計(jì)100位女生中累計(jì)觀看時間小于20個小時的人數(shù).已知200位男生中累計(jì)觀看時間小于20小時的男生有50人請完成答題卡中的列聯(lián)表,并判斷是否有99 %的把握認(rèn)為“該校學(xué)生觀看冬奧會累計(jì)時間與性別有關(guān)”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且
,且![]() ,圓
,圓![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,![]() ,
,![]() 為橢圓
為橢圓![]() 上的動點(diǎn),
上的動點(diǎn),![]() ,
,![]() 面積最大值為
面積最大值為![]() .
.
(1)求圓![]() 與橢圓
與橢圓![]() 的方程;
的方程;
(2)圓![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() ,求四面體
,求四面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)當(dāng)m=1時,求曲線y=f(x)在點(diǎn)(1,f(1))處的切線斜率;
(2)求函數(shù)的單調(diào)區(qū)間與極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的定義域;
的定義域;
(2)若函數(shù)![]() 有且僅有一個零點(diǎn),求實(shí)數(shù)m的取值范圍;
有且僅有一個零點(diǎn),求實(shí)數(shù)m的取值范圍;
(3)任取![]() ,若不等式
,若不等式![]() 對任意
對任意![]() 恒成立,求實(shí)數(shù)m的取值范圍.
恒成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
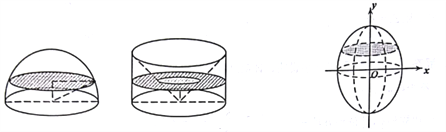
【題目】我國南北朝時間著名數(shù)學(xué)家祖暅提出了祖暅原理:“冪勢既同,則積不容異”.意思是:夾在兩平行平面間的兩個幾何體,被平行于這兩個平行平面的任何平面所載,若截得的兩個截面面積總相等,則這兩個幾何體的體積相等.為計(jì)算球的體積,構(gòu)造一個底面半徑和高都與球半徑相等的圓柱,然后再圓柱內(nèi)挖去一個以圓柱下底面圓心為頂點(diǎn),圓柱上底面為底面的圓錐,運(yùn)用祖暅原理可證明此幾何體與半球體積相等(任何一個平面所載的兩個截面面積都相等).將橢圓![]() 繞
繞![]() 軸旋轉(zhuǎn)一周后得一橄欖狀的幾何體,類比上述方法,運(yùn)用祖暅原理可求得其體積等于( )
軸旋轉(zhuǎn)一周后得一橄欖狀的幾何體,類比上述方法,運(yùn)用祖暅原理可求得其體積等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com