【題目】已知函數
，其中
（Ⅰ）求
的單調區間；
（Ⅱ）若在
上存在
，使得
成立，求
的取值范圍.
【答案】（1）見解析（2）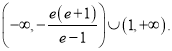
【解析】試題分析：（1）函數的單調區間與導數的符號相關，而函數的導數為
，故可以根據
的符號討論導數的符號，從而得到函數的單調區間.（2）若不等式
在
上有解，那么在
上， 
.但
在
上的單調性不確定，故需分
三種情況討論.
解析：（1）
，
①當
時，在
上
， 
在
上單調遞增；
②當
時，在
上
；在
上
；所以
在
上單調遞減，在
上單調遞增.
綜上所述，當
時， 
的單調遞增區間為
，當
時， 
的單調遞減區間為
，單調遞增區間為
.
（2）若在
上存在
，使得
成立，則
在
上的最小值小于
.
①當
，即
時，由（1）可知
在
上單調遞增， 
在
上的最小值為
，由
，可得
，
②當
，即
時，由（1）可知
在
上單調遞減， 
在
上的最小值為
，由
，可得
；
③當
，即
時，由（1）可知
在
上單調遞減，在
上單調遞增， 
在
上的最小值為
，因為
，所以
，即
，即
，不滿足題意，舍去.
綜上所述，實數
的取值范圍為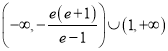
.
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
快樂暑假暑假能力自測中西書局系列答案科目：高中數學 來源： 題型：
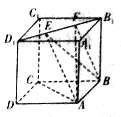
【題目】如圖所示，正方體
的棱長為1，線段
上有兩個動點
，則下列結論中正確結論的序號是__________．
①
；
②直線
與平面
所成角的正弦值為定值
；
③當
為定值，則三棱錐
的體積為定值；
④異面直線
所成的角的余弦值為定值
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，函數
的導函數為
．
⑴ 若直線
與曲線
恒相切于同一定點，求
的方程；
⑵ 若
，求證：當
時， 
恒成立；
⑶ 若當
時， 
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）如圖，在三棱柱ABC－A1B1C1中，側棱垂直于底面，AB⊥BC，E、F分別為A1C1和BC的中點．
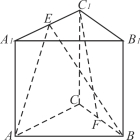
（1）求證：平面ABE⊥平面B1BCC1；
（2）求證：C1F//平面ABE．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f(x)＝(1＋x)m＋(1＋2x)n(m，n∈N*)的展開式中x的系數為11．
(1)求x2的系數取最小值時n的值；
(2)當x2的系數取得最小值時，求f(x)展開式中x的奇次冪項的系數之和．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
