
【題目】記![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函數
.已知函數![]() ,
,![]() .
.
(1)設![]() ,求函數
,求函數![]() 在
在![]() 上零點的個數;
上零點的個數;
(2)試探討是否存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)![]() 個;(2)存在,
個;(2)存在,![]() .
.
【解析】
試題分析:(1)設![]() ,利用導數與單調性的關系求出
,利用導數與單調性的關系求出![]() ,可得
,可得![]() ,則
,則![]() ,結合圖象可得零點的個數;(2)可將題意轉化為
,結合圖象可得零點的個數;(2)可將題意轉化為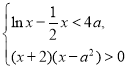 對
對![]() 恒成立,分別求
恒成立,分別求![]() 和
和![]() 成立即可.
成立即可.
試題解析:(1)設![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,![]() 遞增;令
遞增;令![]() ,得
,得![]() ,
,![]() 遞減.
遞減.
∴![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() .
.
設![]() ,結合
,結合![]() 與
與![]() 在
在![]() 上圖象可知,這兩個函數的圖象在
上圖象可知,這兩個函數的圖象在![]() 上有兩個交點,即
上有兩個交點,即![]() 在
在![]() 上零點的個數為
上零點的個數為![]() .
.
(2)假設存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立,
恒成立,
則 對
對![]() 恒成立,
恒成立,
即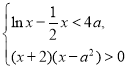 對
對![]() 恒成立,
恒成立,
(i)設![]() ,
,![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() 遞增;令
遞增;令![]() ,得
,得![]() ,
,![]() 遞減.
遞減.
∴![]() .
.
當![]() ,即
,即![]() 時,
時,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
故當![]() 時,
時,![]() 對
對![]() 恒成立.
恒成立.
當![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上遞減,∴
上遞減,∴![]() .
.
∵![]() ,∴
,∴![]()
故當![]() 時,
時,![]() 對
對![]() 恒成立.
恒成立.
(ii)若![]() 對
對![]() 恒成立,則
恒成立,則![]() ,∴
,∴![]() .
.
由(i)及(ii)得,![]() .
.
故存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立,
恒成立,
且![]() 的取值范圍為
的取值范圍為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①函數![]() 的圖象把圓
的圖象把圓![]() 的面積兩等分
的面積兩等分
②![]() 是周期為
是周期為![]() 的函數
的函數
③函數![]() 在區間
在區間![]() 上有3個零點
上有3個零點
④函數![]() 在區間
在區間![]() 上單調遞減
上單調遞減
其中所有正確結論的編號是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.
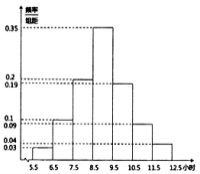
(1)求這200名學生每周閱讀時間的樣本平均數![]() 和中位數
和中位數![]() (
(![]() 的值精確到0.01);
的值精確到0.01);
(2)為查找影響學生閱讀時間的因素,學校團委決定從每周閱讀時間為![]() ,
,![]() 的學生中抽取9名參加座談會.
的學生中抽取9名參加座談會.
(i)你認為9個名額應該怎么分配?并說明理由;
(ii)座談中發現9名學生中理工類專業的較多.請根據200名學生的調研數據,填寫下面的列聯表,并判斷是否有![]() 的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
的把握認為學生閱讀時間不足(每周閱讀時間不足8.5小時)與“是否理工類專業”有關?
閱讀時間不足8.5小時 | 閱讀時間超過8.5小時 | |
理工類專業 | 40 | 60 |
非理工類專業 |
附:![]() (
(![]() ).
).
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于正整數![]() ,如果
,如果![]() 個整數
個整數![]() 滿足
滿足![]() ,
,
且![]() ,則稱數組
,則稱數組![]() 為
為![]() 的一個“正整數分拆”.記
的一個“正整數分拆”.記![]() 均為偶數的“正整數分拆”的個數為
均為偶數的“正整數分拆”的個數為![]() 均為奇數的“正整數分拆”的個數為
均為奇數的“正整數分拆”的個數為![]() .
.
(Ⅰ)寫出整數4的所有“正整數分拆”;
(Ⅱ)對于給定的整數![]() ,設
,設![]() 是
是![]() 的一個“正整數分拆”,且
的一個“正整數分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)對所有的正整數![]() ,證明:
,證明:![]() ;并求出使得等號成立的
;并求出使得等號成立的![]() 的值.
的值.
(注:對于![]() 的兩個“正整數分拆”
的兩個“正整數分拆”![]() 與
與![]() ,當且僅當
,當且僅當![]() 且
且![]() 時,稱這兩個“正整數分拆”是相同的.)
時,稱這兩個“正整數分拆”是相同的.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省GDP情況圖,則下列陳述中不正確的是( )
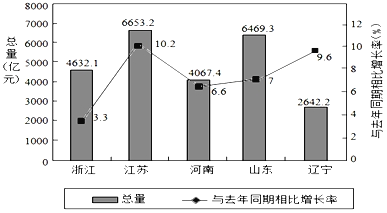
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.與去年同期相比,2017年第一季度的GDP總量實現了增長.
C.2017年第一季度GDP總量和增速由高到低排位均居同一位的省只有1個
D.去年同期河南省的GDP總量不超過4000億元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() 的展開圖如圖二,其中四邊形
的展開圖如圖二,其中四邊形![]() 為邊長等于
為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐
均為正三角形,在三棱錐![]() 中:
中:
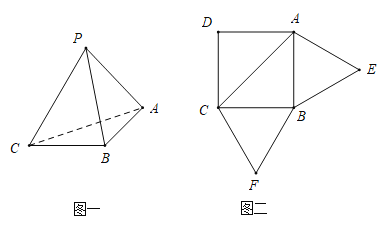
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】購買一輛某品牌新能源汽車,在行駛三年后,政府將給予適當金額的購車補貼.某調研機構對擬購買該品牌汽車的消費者,就購車補貼金額的心理預期值進行了抽樣調查,其樣本頻率分布直方圖如圖所示
.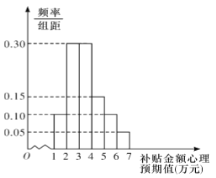
(1)估計擬購買該品牌汽車的消費群體對購車補貼金額的心理預期值的方差(同一組中的數據用該組區間的中點值作代表);
(2)將頻率視為概率,從擬購買該品牌汽車的消費群體中隨機抽取![]() 人,記對購車補貼金額的心理預期值高于
人,記對購車補貼金額的心理預期值高于![]() 萬元的人數為
萬元的人數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)統計最近![]() 個月該品牌汽車的市場銷售量,得其頻數分布表如下:
個月該品牌汽車的市場銷售量,得其頻數分布表如下:
月份 |
|
|
|
|
|
銷售量(萬輛) |
|
|
|
|
|
試預計該品牌汽車在![]() 年
年![]() 月份的銷售量約為多少萬輛?
月份的銷售量約為多少萬輛?
附:對于一組樣本數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為比較甲、乙兩地某月14時的氣溫狀況,隨機選取該月中的5天,將這5天中14時的氣溫數據(單位:℃)制成如圖所示的莖葉圖.考慮以下結論:
①甲地該月14時的平均氣溫低于乙地該月14時的平均氣溫;
②甲地該月14時的平均氣溫高于乙地該月14時的平均氣溫;
③甲地該月14時的平均氣溫的標準差小于乙地該月14時的氣溫的標準差;
④甲地該月14時的平均氣溫的標準差大于乙地該月14時的氣溫的標準差.
其中根據莖葉圖能得到的統計結論的標號為( )
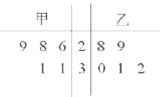
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com