
【題目】如圖,直三棱柱![]() 中,
中,![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明:![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)法一:要證![]() 平面
平面![]() ,只需證明
,只需證明![]() 即可,通過構造平行四邊形可證之;
即可,通過構造平行四邊形可證之;
法二:可先證平面![]() 平面
平面![]() ,利用面面平行的性質即可得到
,利用面面平行的性質即可得到![]() 平面
平面![]() ;
;
(2)法一:由于![]() 即為
即為![]() 與平面
與平面![]() 所成的角,利用數據求之;
所成的角,利用數據求之;
法二:(等積法)利用等積法計算出![]() 到平面
到平面![]() 的距離,從而要求的答案為:
的距離,從而要求的答案為:![]() 即可.
即可.
(1)法一:取![]() 中點
中點![]() ,連接
,連接![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() .
.
∵![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點,∴
中點,∴![]() ,
,
∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() .∵
.∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
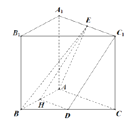
法二:取![]() 中點
中點![]() ,連結
,連結![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() .
.
∵![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點,∴
中點,∴![]() ,
,
∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 分別為
分別為![]() 中點,∴
中點,∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.![]() 平面
平面![]() 平面
平面![]() .
.
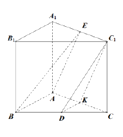
(2)法一:直三棱柱![]() 中,
中,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .
.
過![]() 作
作![]() 于
于![]() .∵
.∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() .
.
又![]() 即為
即為![]() 與平面
與平面![]() 所成的角.
所成的角.
![]() .
.
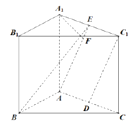
法二:(等積法)![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
連結![]() ,直三棱柱
,直三棱柱![]() 中,
中,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() .
.
![]() ,
,![]() .
.
設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,![]() .
.
∵![]() ,即
,即![]() .
.
設![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,![]() .
.
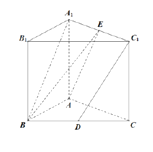


科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率低于![]() ,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃明年用不超過6千萬元的資金投資于本地養魚場和遠洋捕撈隊.經過對本地養魚場年利潤率的調研,其結果是:年利潤虧損10%的概率為0.2,年利潤獲利30%的概率為0.4,年利潤獲利50%的概率為0.4,對遠洋捕撈隊的調研結果是:年利潤獲利為60%的概率為0.7,持平的概率為0.2,年利潤虧損20%的可能性為0.1. 為確保本地的鮮魚供應,市政府要求該公司對遠洋捕撈隊的投資不得高于本地養魚場的投資的2倍.根據調研數據,該公司如何分配投資金額,明年兩個項目的利潤之和最大值為_________千萬.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某中學為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識的競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐、規定:每場知識競賽前三名的得分都分別為![]() (
(![]() ,且
,且![]() );選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為26分,乙和丙最后得分都為11分,且乙在其中一場比賽中獲得第一名,則下列推理正確的是( )
);選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為26分,乙和丙最后得分都為11分,且乙在其中一場比賽中獲得第一名,則下列推理正確的是( )
A. 每場比賽第一名得分![]() 為4 B. 甲可能有一場比賽獲得第二名
為4 B. 甲可能有一場比賽獲得第二名
C. 乙有四場比賽獲得第三名 D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了緩解日益擁堵的交通狀況,不少城市實施車牌競價策略,以控制車輛數量.某地車牌競價的基本規則是:①“盲拍”,即所有參與競拍的人都要網絡報價一次,每個人不知曉其他人的報價,也不知道參與當期競拍的總人數;②競價時間截止后,系統根據當期車牌配額,按照競拍人的出價從高到低分配名額.某人擬參加2018年5月份的車牌競拍,他為了預測最低成交價,根據競拍網站的數據,統計了最近5個月參與競拍的人數(見下表):

(1)由收集數據的散點圖發現,可用線性回歸模型擬合競拍人數y(萬人)與月份編號t之間的相關關系.請用最小二乘法求y關于t的線性回歸方程:![]() ,并預測2018年5月份參與競拍的人數.
,并預測2018年5月份參與競拍的人數.
(2)某市場調研機構從擬參加2018年5月份車牌競拍人員中,隨機抽取了200人,對他們的擬報價價格進行了調查,得到如下頻數分布表和頻率分布直方圖:

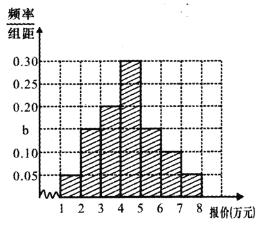
(i)求![]() 的值及這200位竟拍人員中報價大于5萬元的人數;
的值及這200位竟拍人員中報價大于5萬元的人數;
(ii)若2018年5月份車牌配額數量為3000,假設競拍報價在各區間分布是均勻的,請你根據以上抽樣的數據信息,預測(需說明理由)競拍的最低成交價.
參考公式及數據:①![]() ,其中
,其中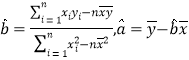 ;
;
②![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點,點
上一點,點![]() 是曲線
是曲線![]() 上一點,
上一點,![]() 的最小值為
的最小值為![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校數學課外興趣小組為研究數學成績是否與性別有關,先統計本校高三年級每個學生一學期數學成績平均分(采用百分制),剔除平均分在![]() 分以下的學生后,共有男生
分以下的學生后,共有男生![]() 名,女生
名,女生![]() 名.現采用分層抽樣的方法,從中抽取了
名.現采用分層抽樣的方法,從中抽取了![]() 名學生,按性別分為兩組,并將兩組學生成績分為
名學生,按性別分為兩組,并將兩組學生成績分為![]() 組,得到如下所示頻數分布表.
組,得到如下所示頻數分布表.
分數段 |
|
|
|
|
|
|
男 |
|
|
|
|
|
|
女 |
|
|
|
|
|
|
(Ⅰ)規定![]() 分以上為優分(含
分以上為優分(含![]() 分),請你根據已知條件作出
分),請你根據已知條件作出![]() 列聯表.
列聯表.
優分 | 非優分 | 合計 | |
男生 | |||
女生 | |||
合計 |
|
(Ⅱ)根據你作出的![]() 列聯表判斷是否有
列聯表判斷是否有![]() 以上的把握認為“數學成績與性別有關”.
以上的把握認為“數學成績與性別有關”.
附表及公式:
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com