
【題目】已知點![]() ,過點
,過點![]() 作與
作與![]() 軸平行的直線
軸平行的直線![]() ,點
,點![]() 為動點
為動點![]() 在直線
在直線![]() 上的投影,且滿足
上的投影,且滿足![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知點![]() 為曲線
為曲線![]() 上的一點,且曲線
上的一點,且曲線![]() 在點
在點![]() 處的切線為
處的切線為![]() ,若
,若![]() 與直線
與直線![]() 相交于點
相交于點![]() ,試探究在
,試探究在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標,若不存在,說明理由.
的坐標,若不存在,說明理由.
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是首項
是首項![]() 的等差數列,設
的等差數列,設![]() .
.
(1)求證:![]() 是等比數列;
是等比數列;
(2)記![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)在(2)的條件下,記![]() ,若對任意正整數
,若對任意正整數![]() ,不等式
,不等式![]() 恒成立,求整數
恒成立,求整數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·江蘇高考)如圖,在三棱錐ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E,F(E與A,D不重合)分別在棱AD,BD上,且EF⊥AD.

求證:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】伴隨著智能手機的深入普及,支付形式日漸多樣化,打破了傳統支付的局限性和壁壘,有研究表明手機支付的使用比例與人的年齡存在一定的關系,某調研機構隨機抽取了50人,對他們一個月內使用手機支付的情況進行了統計,如下表:

(1)若以“年齡55歲為分界點”,由以上統計數據完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“使用手機支付”與人的年齡有關;
的把握認為“使用手機支付”與人的年齡有關;

(2)若從年齡在![]() ,
,![]() 內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為
內的被調查人中各隨機選取2人進行追蹤調查,記選中的4人中“使用手機支付”的人數為![]() .
.
①求隨機變量![]() 的分布列;
的分布列;
②求隨機變量![]() 的數學期望.
的數學期望.
參考數據如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
參考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是 (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
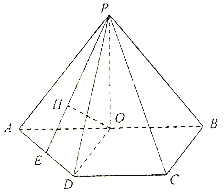
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中點,
的中點,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影為點
上的正投影為點![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() 為
為![]() 中點;
中點;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com