
【題目】函數![]() 圖象上不同兩點
圖象上不同兩點![]() ,
,![]() 處切線的斜率分別是
處切線的斜率分別是![]() ,
,![]() 規定
規定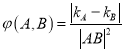 (
(![]() 為線段
為線段![]() 的長度)叫做曲線
的長度)叫做曲線![]() 在點
在點![]() 與
與![]() 之間的“平方彎曲度”,給出以下命題:
之間的“平方彎曲度”,給出以下命題:
①函數![]() 圖象上兩點
圖象上兩點![]() 與
與![]() 的橫坐標分別為1和2,則
的橫坐標分別為1和2,則![]() ;
;
②存在這樣的函數,圖象上任意兩點之間的“平方彎曲度”為常數;
③設點![]() ,
,![]() 是拋物線
是拋物線![]() 上不同的兩點,則
上不同的兩點,則![]() ;
;
④設曲線![]() (
(![]() 是自然對數的底數)上不同兩點
是自然對數的底數)上不同兩點![]() ,
,![]() ,且
,且![]() ,則
,則![]() 的最大值為
的最大值為![]() .
.
其中真命題的序號為__________(將所有真命題的序號都填上)
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,M是SB的中點,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
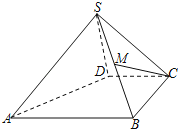
(1)證明:CD⊥SD;
(2)證明:CM∥面SAD;
(3)求四棱錐S﹣ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某面包店隨機收集了面包種類的有關數據,經分類整理得到下表:
面包類型 | 第一類 | 第二類 | 第三類 | 第四類 | 第五類 | 第六類 |
面包個數 | 90 | 60 | 30 | 80 | 100 | 40 |
好評率 | 0.6 | 0.45 | 0.7 | 0.35 | 0.6 | 0.5 |
好評率是指:一類面包中獲得好評的個數與該類面包的個數的比值.
(1)從面包店收集的面包中隨機選取1個,求這個面包是獲得好評的第五類面包的概率;
(2)從面包店收集的面包中隨機選取1個,估計這個面包沒有獲得好評的概率;
(3)面包店為增加利潤,擬改變生產策略,這將導致不同類型面包的好評率發生變化.假設表格中只有兩類面包的好評率數據發生變化,那么哪類面包的好評率增加0.1,哪類面包的好評率減少0.1,使得獲得好評的面包總數與樣本中的面包總數的比值達到最大?(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與直線
與直線![]() 相切于點
相切于點![]() ,圓心
,圓心![]() 在
在![]() 軸上.
軸上.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 且不與
且不與![]() 軸重合的直線
軸重合的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,
兩點,![]() 為坐標原點,直線
為坐標原點,直線![]() 分別與直線
分別與直線![]() 相交于
相交于![]() 兩點,記
兩點,記![]() ,
,![]() 的面積分別是
的面積分別是![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓![]() (a>1).
(a>1).
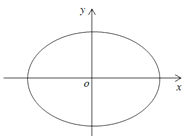
(Ⅰ)求直線y=kx+1被橢圓截得的線段長(用a、k表示);
(Ⅱ)若任意以點A(0,1)為圓心的圓與橢圓至多有3個公共點,求橢圓離心率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年7月9日21時15分,臺風“蓮花”在我國廣東省陸豐市甲東鎮沿海登陸,造成165.17萬人受災,5.6萬人緊急轉移安置,288間房屋倒塌,46.5千公頃農田受災,直接經濟損失12.99億元.距離陸豐市222千米的梅州也受到了臺風的影響,適逢暑假,小明調查了梅州某小區的50戶居民由于臺風造成的經濟損失,將收集的數據分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五組,并作出如圖頻率分布直方圖:
五組,并作出如圖頻率分布直方圖:
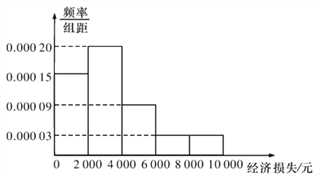
(1)試根據頻率分布直方圖估計小區平均每戶居民的平均損失(同一組中的數據用該組區間的中點值代表);
(2)小明向班級同學發出倡議,為該小區居民捐款,現從損失超過4000元的居民中隨機抽取2戶進行捐款援助,設抽出損失超過8000元的居民為![]() 戶,求
戶,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)臺風后區委會號召小區居民為臺風重災區捐款,小明調查的50戶居民捐款情況如圖,根據圖表格中所給數據,分別求![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值,并說明是否有
的值,并說明是否有![]() 以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
經濟損失不超過4000元 | 經濟損失超過4000元 | 合計 | |
捐款超過500元 |
|
| |
捐款不超過500元 |
|
| |
合計 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:臨界值表參考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動點![]() 到定點
到定點![]() 的距離之比它到直線
的距離之比它到直線![]() 的距離小1,設動點
的距離小1,設動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 的直線交曲線
的直線交曲線![]() 于
于![]() 兩個不同的點,過點
兩個不同的點,過點![]() 分別作曲線
分別作曲線![]() 的切線,且二者相交于點
的切線,且二者相交于點![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)求證:![]() ;
;
(3)求![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com