經(jīng)過拋物線
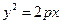
的焦點
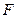
作一直線,和拋物線相交于
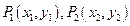
,求
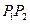
的長。
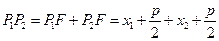
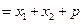
。
名師點金:原題中的焦點弦是垂直于對稱軸的,這樣的焦點弦稱為通徑,它的長為
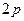
,變成任一條焦點弦后,利用拋物線的定義可得
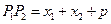
,事實上,原題是變式的一種特殊情況:即
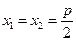
時,
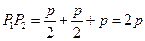
。另外,此題還可以變成:過焦點
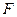
作一傾角為
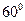
的直線
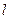
交拋物線于
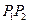
兩點,求
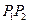
的長,此時
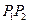
的長仍然為
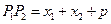
,但要把直線的方程與拋物線的方程聯(lián)立后,消去
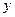
得關于
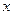
的一元二次方程,從而利用韋達定理得到

,最后得到
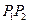
的長。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
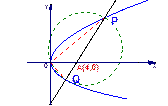
已知直線
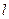
過定點A(4,0)且與拋物線
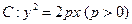
交于P、Q兩點,若以PQ為直徑的圓恒過原點O,求
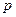
的值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
已知拋物線以原點為頂點,以
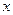
軸為對稱軸,焦點在直線
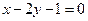
上.
(1)求拋物線的方程;(2)設
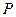
是拋物線上一點,點
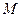
的坐標為
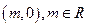
,求
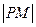
的最小值(用
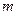
表示),并指出此時點
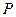
的坐標。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
拋物線的頂點在原點,焦點是圓
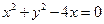
的圓心,(1)求拋物線的方程;(2)直線
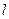
的斜率為
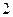
,且過拋物線的焦點,若
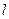
與拋物線、圓依次交于
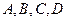
四個點,求
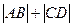
。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
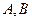
是拋物線
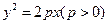
上兩點,
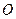
為坐標原點,若
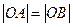
,且
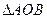
的垂心恰是此拋物線的焦點,則直線
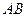
的方程是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設頂點在原點,焦點在
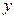
軸上的拋物線上的一點
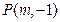
到焦點的距離為
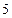
,則
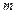
的值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知定點A(3,4),點P為拋物線
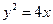
上一動點,點P到直線
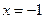
的距離為
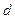
,則
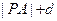
的最小值為
| A.4 | B.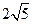 | C.6 | D.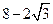 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
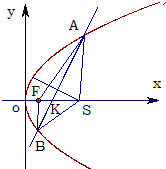
已知拋物線y
2=2px(p>0),焦點為F,一直線l與拋物線交于A、B兩點,且|AF|+|BF|=8,且AB的垂直平分線恒過定點S(6,0)
①求拋物線方程;
②求△ABS面積的最大值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設點A為拋物線
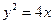
上一點,點B的坐標為
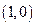
,且
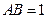
,則點

的橫坐標的值為( )
查看答案和解析>>

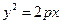 的焦點
的焦點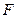 作一直線,和拋物線相交于
作一直線,和拋物線相交于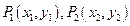 ,求
,求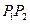 的長。
的長。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案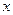 軸為對稱軸,焦點在直線
軸為對稱軸,焦點在直線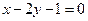 上.
上.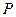 是拋物線上一點,點
是拋物線上一點,點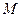 的坐標為
的坐標為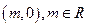 ,求
,求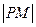 的最小值(用
的最小值(用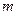 表示),并指出此時點
表示),并指出此時點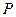 的坐標。
的坐標。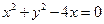 的圓心,(1)求拋物線的方程;(2)直線
的圓心,(1)求拋物線的方程;(2)直線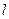 的斜率為
的斜率為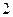 ,且過拋物線的焦點,若
,且過拋物線的焦點,若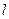 與拋物線、圓依次交于
與拋物線、圓依次交于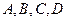 四個點,求
四個點,求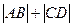 。
。