
【題目】某商場舉行的“三色球”購物摸獎活動規定:在一次摸獎中,摸獎者先從裝有3個紅球與4個白球的袋中任意摸出3個球,再從裝有1個藍球與2個白球的袋中任意摸出1個球,根據摸出4個球中紅球與藍球的個數,設一、二、三等獎如下:
獎級 | 摸出紅、藍球個數 | 獲獎金額 |
一等獎 | 3紅1藍 | 200元 |
二等獎 | 3紅0藍 | 50元 |
三等獎 | 2紅1藍 | 10元 |
其余情況無獎且每次摸獎最多只能獲得一個獎級.
(1)求一次摸獎恰好摸到1個紅球的概率;
(2)求摸獎者在一次摸獎中獲獎金額x的分布列與期望E(x).
【答案】
(1)解:設Ai表示摸到i個紅球,Bi表示摸到i個藍球,則Ai與Bi相互獨立(i=0,1,2,3)
∴P(A1)= ![]() =
= ![]()
(2)解:X的所有可能取值為0,10,50,200
P(X=200)=P(A3B1)=P(A3)P(B1)= ![]()
P(X=50)=P(A3)P(B0)= ![]() =
= ![]()
P(X=10)=P(A2)P(B1)= ![]() =
= ![]()
P(X=0)=1﹣ ![]() =
= ![]()
∴X的分布列為
x | 0 | 10 | 50 | 200 |
P |
|
|
|
|
EX= ![]() =4元
=4元
【解析】(1)從7個小球中取3的取法為 ![]() ,若取一個紅球,則說明第一次取到一紅2白,根據組合知識可求取球的種數,然后代入古典概率計算公式可求(2)先判斷隨機變量X的所有可能取值為200,50,10,0根據題意求出隨機變量的各個取值的概率,即可求解分布列及期望值
,若取一個紅球,則說明第一次取到一紅2白,根據組合知識可求取球的種數,然后代入古典概率計算公式可求(2)先判斷隨機變量X的所有可能取值為200,50,10,0根據題意求出隨機變量的各個取值的概率,即可求解分布列及期望值


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在空間直角坐標系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1, ![]() ),若S1 , S2 , S3分別表示三棱錐D﹣ABC在xOy,yOz,zOx坐標平面上的正投影圖形的面積,則( )
),若S1 , S2 , S3分別表示三棱錐D﹣ABC在xOy,yOz,zOx坐標平面上的正投影圖形的面積,則( )
A.S1=S2=S3
B.S2=S1且S2≠S3
C.S3=S1且S3≠S2
D.S3=S2且S3≠S1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(2ωx+![]() )+sin(2ωx-
)+sin(2ωx-![]() )+2cos2ωx,其中ω>0,且函數f(x)的最小正周期為π
)+2cos2ωx,其中ω>0,且函數f(x)的最小正周期為π
(1)求ω的值;
(2)求f(x)的單調增區間
(3)若函數g(x)=f(x)-a在區間[-![]() ,
,![]() ]上有兩個零點,求實數a的取值范圍.
]上有兩個零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓的中心為原點O,長軸在x軸上,離心率 ![]() ,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4.
,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4. 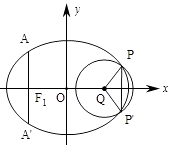
(1)求該橢圓的標準方程;
(2)取垂直于x軸的直線與橢圓相交于不同的兩點P、P′,過P、P′作圓心為Q的圓,使橢圓上的其余點均在圓Q外.若PQ⊥P'Q,求圓Q的標準方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對正整數n,記In={1,2,3…,n},Pn={ ![]() |m∈In , k∈In}.
|m∈In , k∈In}.
(1)求集合P7中元素的個數;
(2)若Pn的子集A中任意兩個元素之和不是整數的平方,則稱A為“稀疏集”.求n的最大值,使Pn能分成兩個不相交的稀疏集的并集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某市組織的一次數學競賽中全體參賽學生的成績近似服從正態分布N(60,100),已知成績在90分以上的學生有13人.
(1)求此次參加競賽的學生總數共有多少人?
(2)若計劃獎勵競賽成績排在前228名的學生,問受獎學生的分數線是多少?
(參考數據:若![]() ,則
,則![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2lnx.
(1)求函數f(x)的單調區間;
(2)證明:對任意的t>0,存在唯一的s,使t=f(s).
(3)設(2)中所確定的s關于t的函數為s=g(t),證明:當t>e2時,有 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com