
【題目】某家電專賣店試銷A、B、C三種新型空調,連續五周銷售情況如表所示:
第一周 第二周 第三周 第四周 第五周
A型數量/臺 12 8 15 22 18
B型數量/臺 7 12 10 10 12
C型數量/臺 ![]()
![]()
![]()
![]()
![]()
(I)求A型空調平均每周的銷售數量;
(Ⅱ)為跟蹤調查空調的使用情況,從該家電專賣店第二周售出的A、B型空調銷售記錄中,隨機抽取一臺,求抽到B型空調的概率;
(III)已知C型空調連續五周銷量的平均數為7,方差為4,且每周銷售數量![]() 互不相同,求C型空調這五周中的最大銷售數量。(只需寫出結論)
互不相同,求C型空調這五周中的最大銷售數量。(只需寫出結論)
【答案】(I)15臺;(Ⅱ)![]() ;(Ⅲ)10臺
;(Ⅲ)10臺
【解析】
(I)根據題中數據,結合平均數的計算公式,即可求出結果;
(Ⅱ)先設“隨機抽取一臺,抽到B型空調”為事件D,再由題中數據,確定事件D包含的基本事件個數,以及總的基本事件個數,基本事件個數比即為所求概率;
(III)先根據題意,設![]() ,結合平均數與方差得到
,結合平均數與方差得到![]() ,求出
,求出![]() 范圍,分別取
范圍,分別取![]() 驗證,直到得到符合題意的數據為止.
驗證,直到得到符合題意的數據為止.
(I)A型空調平均每周的銷售數量![]() (臺)
(臺)
(Ⅱ)設“隨機抽取一臺,抽到B型空調”為事件D,
則事件D包含12個基本事件,而所有基本事件個數為![]() ,所以
,所以![]()
(Ⅲ)由于C型空調的每周銷售數量![]() 互不相同,
互不相同,
所以不妨設![]() ,因為C型空調連續五周銷量的平均數為7,方差為4,
,因為C型空調連續五周銷量的平均數為7,方差為4,
所以![]() ,
,
為了讓C型空調這五周中的最大周銷售數量最大,即只需讓![]() 最大即可,
最大即可,
由于![]() ,所以易知
,所以易知![]() ,
,
當![]() 時,由于
時,由于![]()
所以![]()
此時必然有![]() ,而與題目中所要求的每周銷售數量
,而與題目中所要求的每周銷售數量![]() 互不相同矛盾,故
互不相同矛盾,故![]() .
.
當![]() 時,由于
時,由于![]() ,
,
所以![]() ,且
,且![]()
若不存在![]() 的情況,則
的情況,則![]() 的最大值為
的最大值為![]() ,
,
所以必有![]() ,即
,即![]() ,
,
而此時![]() ,易知
,易知![]() ,符合題意,故C型空調的五周中的最大周銷售數量為10臺.
,符合題意,故C型空調的五周中的最大周銷售數量為10臺.


科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,已知側面ABB1A1是菱形,側面BCC1B1是正方形,點A1在底面ABC的投影為AB的中點D. 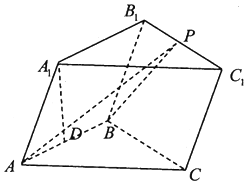
(1)證明:平面AA1B1B⊥平面BB1C1C;
(2)設P為B1C1上一點,且 ![]() ,求二面角A1﹣AB﹣P的正弦值.
,求二面角A1﹣AB﹣P的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】抽樣統計甲、乙兩名學生的5次訓練成績(單位:分),結果如下:
學生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 65 | 80 | 70 | 85 | 75 |
乙 | 80 | 70 | 75 | 80 | 70 |
則成績較為穩定(方差較小)的那位學生成績的方差為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠新研發了一種產品,該產品每件成本為5元,將該產品按事先擬定的價格進行銷售,得到如下數據:
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求銷量![]() (件)關于單價
(件)關于單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(2)若單價定為10元,估計銷量為多少件;
(3)根據銷量![]() 關于單價
關于單價![]() 的線性回歸方程,要使利潤
的線性回歸方程,要使利潤![]() 最大,應將價格定為多少?
最大,應將價格定為多少?
參考公式: ,
,![]() .參考數據:
.參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某公司為鄭州園博園生產某特許商品,該公司年固定成本為10萬元,每生產千件需另投入2 .7萬元,設該公司年內共生產該特許商品工x千件并全部銷售完;每千件的銷售收入為R(x)萬元,
且 ,
,
(I)寫出年利潤W(萬元〉關于該特許商品x(千件)的函數解析式;
〔II〕年產量為多少千件時,該公司在該特許商品的生產中所獲年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差d不為0,且 ![]() ,
, ![]() ,…,
,…, ![]() ,…(k1<k2<…<kn<…)成等比數列,公比為q.
,…(k1<k2<…<kn<…)成等比數列,公比為q.
(1)若k1=1,k2=3,k3=8,求 ![]() 的值;
的值;
(2)當 ![]() 為何值時,數列{kn}為等比數列;
為何值時,數列{kn}為等比數列;
(3)若數列{kn}為等比數列,且對于任意n∈N* , 不等式 ![]() 恒成立,求a1的取值范圍.
恒成立,求a1的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:如果函數f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)滿足 ![]() ,
, ![]() 則稱函數f(x)是[a,b]上的“中值函數”.已知函數
則稱函數f(x)是[a,b]上的“中值函數”.已知函數 ![]() 是[0,m]上的“中值函數”,則實數m的取值范圍是( )
是[0,m]上的“中值函數”,則實數m的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com