
【題目】已知數列![]() 是各項均為正數且公比不等于1的等比數列
是各項均為正數且公比不等于1的等比數列![]() ,對于函數
,對于函數![]() ,若數列
,若數列![]() 為等差數列,則稱函數
為等差數列,則稱函數![]() 為“保比差數列函數”,現有定義在
為“保比差數列函數”,現有定義在![]() 上的如下函數:①
上的如下函數:①![]() ,②
,②![]() ,③
,③![]() ;④
;④![]() ,則為“保比差數列函數”的所有序號為( )
,則為“保比差數列函數”的所有序號為( )
A.①②B.①②④C.③④D.①②③④
【答案】B
【解析】
設數列{an}的公比為q(q≠1),利用保比差數列函數的定義,逐項驗證數列{lnf(an)}為等差數列,即可得到結論.
設數列{an}的公比為q(q≠1)
①由題意,lnf(an)=ln![]() ,∴lnf(an+1)﹣lnf(an)=ln
,∴lnf(an+1)﹣lnf(an)=ln![]() ln
ln![]() ln
ln![]() lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
②由題意,lnf(an)=ln![]() ,∴lnf(an+1)﹣lnf(an)=ln
,∴lnf(an+1)﹣lnf(an)=ln![]() ln
ln![]() lnq2=2lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
lnq2=2lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
③由題意,lnf(an)=ln![]() ,∴lnf(an+1)﹣lnf(an)=ln
,∴lnf(an+1)﹣lnf(an)=ln![]() ln
ln![]() an+1﹣an不是常數,∴數列{lnf(an)}不為等差數列,不滿足題意;
an+1﹣an不是常數,∴數列{lnf(an)}不為等差數列,不滿足題意;
④由題意,lnf(an)=ln![]() ,∴lnf(an+1)﹣lnf(an)=ln
,∴lnf(an+1)﹣lnf(an)=ln![]() ln
ln![]() lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
lnq是常數,∴數列{lnf(an)}為等差數列,滿足題意;
綜上,為“保比差數列函數”的所有序號為①②④
故選:B.


 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
【題目】已知動直線l:(m+3)x-(m+2)y+m=0與圓C:(x-3)2+(y-4)2=9.
(1)求證:無論m為何值,直線l總過定點A,并說明直線l與圓C總相交.
(2)m為何值時,直線l被圓C所截得的弦長最小?請求出該最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中的一個橢圓,它的中心在原點,左焦點為
中的一個橢圓,它的中心在原點,左焦點為![]() ,右頂點為
,右頂點為![]() ,
,
(1)求該橢圓的標準方程;
(2)(文)若![]() 是橢圓上的動點,過P作垂直于x軸的垂線,垂足為M,延長MP至N,使得P恰好為MN中點,求點N的軌跡方程;
是橢圓上的動點,過P作垂直于x軸的垂線,垂足為M,延長MP至N,使得P恰好為MN中點,求點N的軌跡方程;
(理)若已知點![]() ,
,![]() 是橢圓上的動點,求線段
是橢圓上的動點,求線段![]() 中點
中點![]() 的軌跡方程;
的軌跡方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某學校擬建一塊五邊形區域的“讀書角”,三角形區域ABE為書籍擺放區,沿著AB、AE處擺放折線形書架(書架寬度不計),四邊形區域為BCDE為閱讀區,若∠BAE=60°,∠BCD=∠CDE=120°,DE=3BC=3CD=![]() m.
m.
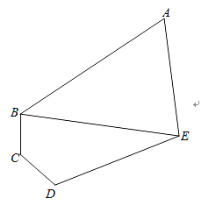
(1)求兩區域邊界BE的長度;
(2)若區域ABE為銳角三角形,求書架總長度AB+AE的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取M名學生作為樣本,得到這M名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表如下,頻率分布直方圖如圖:
分組 | 頻數 | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合計 | M | 1 |

(1)求出表中M,p及圖中a的值;
(2)若該校高三學生有240人,試估計該校高三學生參加社區服務的次數在區間[10,15)內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至多一人參加社區服務次數在區間[25,30)內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com