
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 的準線為
的準線為![]() ,其焦點為F,點B是拋物線C上橫坐標為
,其焦點為F,點B是拋物線C上橫坐標為![]() 的一點,若點B到
的一點,若點B到![]() 的距離等于
的距離等于![]() .
.
(1)求拋物線C的方程,
(2)設A是拋物線C上異于頂點的一點,直線AO交直線![]() 于點M,拋物線C在點A處的切線m交直線
于點M,拋物線C在點A處的切線m交直線![]() 于點N,求證:以點N為圓心,以
于點N,求證:以點N為圓心,以![]() 為半徑的圓經過
為半徑的圓經過![]() 軸上的兩個定點.
軸上的兩個定點.
【答案】(1)![]() ;(2)定點
;(2)定點![]() ,
,![]()
【解析】
(1) 由題意,得![]() ,則△BOF為等腰三角形,求出線段OF的中點的橫坐標即可得到拋物線C的方程;
,則△BOF為等腰三角形,求出線段OF的中點的橫坐標即可得到拋物線C的方程;
(2) 設切線m的方程為:![]() ,聯立方程,借助韋達定理可得
,聯立方程,借助韋達定理可得![]() ,再求出
,再求出![]() ,表示以
,表示以![]() 為半徑的圓的方程即可得到兩個定點.
為半徑的圓的方程即可得到兩個定點.
(1)由題意,得![]() ,則△BOF為等腰三角形,
,則△BOF為等腰三角形,
因為點B的橫坐標為![]() ,所以線段OF的中點的橫坐標為
,所以線段OF的中點的橫坐標為![]() ,
,
從而點F的橫坐標為1,即![]() ,所以p=2,
,所以p=2,
故所求拋物線C的方程為![]() ;
;
(2)證明:設切線m的方程為:![]() ,由
,由![]()
![]() (*)
(*)
由題意知![]() ,即
,即![]()
所以方程(*)的根為 ![]() ,從而
,從而![]() ,
,
直線OA的方程為![]()
由 ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
所以以點N為圓心,以![]() 為半徑的圓的方程為
為半徑的圓的方程為![]() ,
,
令![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以圓N經過x軸上的兩個定點![]() 和
和![]() .
.


科目:高中數學 來源: 題型:
【題目】圓錐![]() (其中
(其中![]() 為頂點,
為頂點,![]() 為底面圓心)的側面積與底面積的比是
為底面圓心)的側面積與底面積的比是![]() ,則圓錐
,則圓錐![]() 與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
與它外接球(即頂點在球面上且底面圓周也在球面上)的體積比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家統計局統計了我國近10年(2009年2018年)的GDP(GDP是國民經濟核算的核心指標,也是衡量一個國家或地區總體經濟狀況的重要指標)增速的情況,并繪制了下面的折線統計圖.

根據該折線統計圖,下面說法錯誤的是
A. 這10年中有3年的GDP增速在9.00%以上
B. 從2010年開始GDP的增速逐年下滑
C. 這10年GDP仍保持6.5%以上的中高速增長
D. 2013年—2018年GDP的增速相對于2009年—2012年,波動性較小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的內接等邊三角形
的內接等邊三角形![]() 的面積為
的面積為![]() (其中
(其中![]() 為坐標原點).
為坐標原點).
(1)試求拋物線![]() 的方程;
的方程;
(2)已知點![]() 兩點在拋物線
兩點在拋物線![]() 上,
上,![]() 是以點
是以點![]() 為直角頂點的直角三角形.
為直角頂點的直角三角形.
①求證:直線![]() 恒過定點;
恒過定點;
②過點![]() 作直線
作直線![]() 的垂線交
的垂線交![]() 于點
于點![]() ,試求點
,試求點![]() 的軌跡方程,并說明其軌跡是何種曲線.
的軌跡方程,并說明其軌跡是何種曲線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數![]() (其中
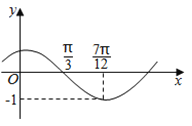
(其中![]() )的圖象如圖所示,為了得到
)的圖象如圖所示,為了得到![]() 的圖象,則只要將
的圖象,則只要將![]() 的圖象上所有的點( )
的圖象上所有的點( )
A.向左平移![]() 個單位長度,縱坐標縮短到原來的
個單位長度,縱坐標縮短到原來的![]() ,橫坐標不變
,橫坐標不變
B.向左平移![]() 個單位長度,縱坐標伸長到原來的3倍橫坐標不變
個單位長度,縱坐標伸長到原來的3倍橫坐標不變
C.向右平移![]() 個單位長度,縱坐標縮短到原來的
個單位長度,縱坐標縮短到原來的![]() ,橫坐標不變
,橫坐標不變
D.向右平移![]() 個單位長度,縱坐標伸長到原來的3倍,橫坐標不變
個單位長度,縱坐標伸長到原來的3倍,橫坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠加工的零件按箱出廠,每箱有10個零件,在出廠之前需要對每箱的零件作檢驗,人工檢驗方法如下:先從每箱的零件中隨機抽取4個零件,若抽取的零件都是正品或都是次品,則停止檢驗;若抽取的零件至少有1個至多有3個次品,則對剩下的6個零件逐一檢驗.已知每個零件檢驗合格的概率為0.8,每個零件是否檢驗合格相互獨立,且每個零件的人工檢驗費為2元.
(1)設1箱零件人工檢驗總費用為![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工檢驗方法外還有機器檢驗方法,機器檢驗需要對每箱的每個零件作檢驗,每個零件的檢驗費為1.6元.現有1000箱零件需要檢驗,以檢驗總費用的數學期望為依據,在人工檢驗與機器檢驗中,應該選擇哪一個?說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 上任意一點到兩個焦點的距離和為4,且離心率為
上任意一點到兩個焦點的距離和為4,且離心率為![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)過![]() 作互相垂直的兩條直線分別與橢圓
作互相垂直的兩條直線分別與橢圓![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() ,設
,設![]() 中點為
中點為![]() ,
,![]() 中點為
中點為![]() ,試探究直線
,試探究直線![]() 是否過定點?若是,求出該定點;若不是,說明理由.
是否過定點?若是,求出該定點;若不是,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com