
【題目】如圖,在四棱錐P﹣ABCD中,底面四邊形ABCD內接于圓O,AC是圓O的一條直徑,PA⊥平面ABCD,PA=AC=2,E是PC的中點,∠DAC=∠AOB 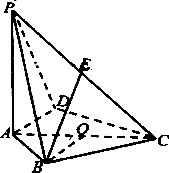
(1)求證:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值為2,求直線PB與平面PCD所成角的正弦值.
【答案】
(1)證明:∵,∠DAC=∠AOB
∴AD∥OB,
∵E是PC的中點,O是AC的中點,
∴OE是△PAC的中位線,
∴OE∥PA,
∵PA∩AD=A,
平面OBE∥平面PAD,
∵BE平面PAD,BE平面PAD,
∴BE∥平面PAD
(2)解:∵AC是圓O的一條直徑,∴AC⊥AD,
∵PA⊥平面ABCD,∴PA⊥CD,
則CD⊥平面PAD,
則CD⊥PD,
則∠PDA是二面角P﹣CD﹣A的平面角,
若二面角P﹣CD﹣A的正切值為2,
則tan∠PDA= ![]() =2,
=2,
即AD=1,
建立以D為坐標原點,DA,DC,垂直于平面ABCD的直線分別為x,y,z軸的空間直角坐標系如圖:
則B( ![]() ,
, ![]() ,0),P(1,0,2),
,0),P(1,0,2), ![]() =(-
=(- ![]() ,﹣
,﹣ ![]() ,2)
,2)
D(0,0,0),C(0, ![]() ,0),
,0),
則 ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(1,0,2),
=(1,0,2),
設平面PCD的法向量為 ![]() =(x,y,z),
=(x,y,z),
則 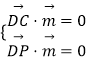 ,即
,即 ![]() ,令z=1,則x=﹣2,y=0,
,令z=1,則x=﹣2,y=0,
即 ![]() =(﹣2,0,1),
=(﹣2,0,1),
則直線PB與平面PCD所成角的正弦值sin< ![]() ,
, ![]() >=|cos<
>=|cos< ![]() ,
, ![]() >|=|
>|=| 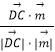 |=
|= ![]()
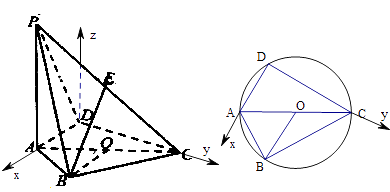
【解析】(1)根據面面平行的性質定理證明平面OBE∥平面PAD,即可證明BE∥平面PAD;(2)建立空間坐標系,根據二面角P﹣CD﹣A的正切值為2,得到AD=1,然后求出平面的法向量,利用直線和平面所成角的定義即可求直線PB與平面PCD所成角的正弦值
【考點精析】本題主要考查了直線與平面平行的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐S﹣ABCD,SB⊥AD,側面SAD是邊長為4的等邊三角形,底面ABCD為菱形,側面SAD與底面ABCD所成的二面角為120°.
(1)求點S到平面ABCD的距離;
(2)若E為SC的中點,求二面角A﹣DE﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C:ρsin2θ=2acosθ(a>0),直線l的參數方程為  (t為參數),l與C分別交于M,N,P(﹣2,﹣4).
(t為參數),l與C分別交于M,N,P(﹣2,﹣4).
(1)寫出C的平面直角坐標系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比數列,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() 圖象上有且僅有四個不同的點關于直線y=e的對稱點在函數g(x)=kx+2e+1的圖象上,則實數k的取值范圍為( )
圖象上有且僅有四個不同的點關于直線y=e的對稱點在函數g(x)=kx+2e+1的圖象上,則實數k的取值范圍為( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩俱樂部舉行乒乓球團體對抗賽.雙方約定:
①比賽采取五場三勝制(先贏三場的隊伍獲得勝利.比賽結束)
②雙方各派出三名隊員.前三場每位隊員各比賽﹣場
已知甲俱樂部派出隊員A1、A2 . A3 , 其中A3只參加第三場比賽.另外兩名隊員A1、A2比賽場次未定:乙俱樂部派出隊員B1、B2 . B3 , 其中B1參加第一場與第五場比賽.B2參加第二場與第四場比賽.B3只參加第三場比賽
根據以往的比賽情況.甲俱樂部三名隊員對陣乙俱樂部三名隊員獲勝的概率如表:
A1 | A2 | A3 | |
B1 |
|
|
|
B2 |
|
|
|
B3 |
|
|
|
(1)若甲俱樂部計劃以3:0取勝.則應如何安排A1、A2兩名隊員的出場順序.使得取勝的概率最大?
(2)若A1參加第一場與第四場比賽,A2參加第二場與第五場比賽,各隊員每場比賽的結果互不影響,設本次團體對抗賽比賽的場數為隨機變量X,求X的分布列及數學期望E(X)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax﹣ ![]() x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲線y=f(x)與y=g(x)在原點處的公共的切線.
x2﹣aln(x+1)(a>0),g(x)=ex﹣x﹣1,曲線y=f(x)與y=g(x)在原點處的公共的切線.
(1)若x=0為函數f(x)的極大值點,求f(x)的單調區間(用a表示);
(2)若x≥0,g(x)≥f(x)+ ![]() x2 , 求a的取值范圍.
x2 , 求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,我國許多省市霧霾天氣頻發,為增強市民的環境保護意識,某市面向全市征召n名義務宣傳志愿者,成立環境保護宣傳組織![]() 現把該組織的成員按年齡分成5組:第1組
現把該組織的成員按年齡分成5組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示,已知第2組有70人.
,得到的頻率分布直方圖如圖所示,已知第2組有70人.
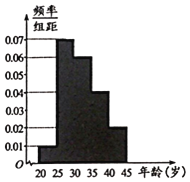
(1)求該組織的人數.
(2)若從第3,4,5組中用分層抽樣的方法抽取6名志愿者參加某社區的宣傳活動,然后在這6名志愿者中隨機抽取2名志愿者介紹宣傳經驗,求第3組至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某重點中學將全部高一學生分成![]() 兩個成績相當(成績的均值、方差都相同)的級部,
兩個成績相當(成績的均值、方差都相同)的級部, ![]() 級部采用傳統形式的教學方式,
級部采用傳統形式的教學方式, ![]() 級部采用新型的基于信息化的自主學習教學方式.為了解教學效果,期末考試后分別從兩個級部中各隨機抽取30名學生的數學成績進行統計,做出莖葉圖如下,記成績不低于127分者為“優秀”.
級部采用新型的基于信息化的自主學習教學方式.為了解教學效果,期末考試后分別從兩個級部中各隨機抽取30名學生的數學成績進行統計,做出莖葉圖如下,記成績不低于127分者為“優秀”.
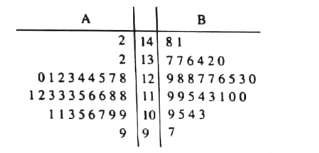
(1)在![]() 級部樣本的30個個體中隨機抽取1個,求抽出的為“優秀”的概率;
級部樣本的30個個體中隨機抽取1個,求抽出的為“優秀”的概率;
(2)由以上數據填寫下面列聯表,并判斷是否有![]() 的把握認為“優秀”與教學方式有關.
的把握認為“優秀”與教學方式有關.
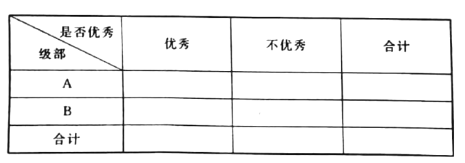
附表:

附: 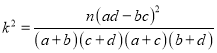 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com