
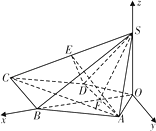
【題目】如圖,已知四棱錐S﹣ABCD,SB⊥AD,側面SAD是邊長為4的等邊三角形,底面ABCD為菱形,側面SAD與底面ABCD所成的二面角為120°.
(1)求點S到平面ABCD的距離;
(2)若E為SC的中點,求二面角A﹣DE﹣C的正弦值.
【答案】
(1)
解:如圖,作SO⊥平面ABCD,垂足為點O.
連接OB,OA,OD,OB與AD交于點F,連接SF.
∵SB⊥AD,
∴OB⊥AD.
∵SA=SD,
∴OA=OD.
∴點F為AD的中點,所以SF⊥AD.
由此知∠SFB為側面SAD與底面ABCD所成的二面角的平面角,
∴∠SFB=120°,
∵側面SAD是邊長為4的等邊三角形,
∴SF= ![]() =2
=2 ![]() ,
,
∴SO=SFsin60°=2 ![]() =3,
=3,
即點S到平面ABCD的距離為3
(2)
解:如圖以O為坐標原點,使y軸與BC平行,OB,OS所在直線分別為y軸、z軸建立空間直角坐標系,
由已知得:A( ![]() ,2,0),D(
,2,0),D( ![]() ,0),C(3
,0),C(3 ![]() ,﹣4,0),E(
,﹣4,0),E( ![]() ,﹣2,
,﹣2, ![]() ),
),
![]() =(0,﹣4,0),
=(0,﹣4,0), ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,2,
,2, ![]() ),
),
設平面ADE的法向量為 ![]() ,
,
則 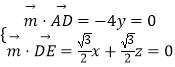 令x=
令x= ![]() ,得
,得 ![]() =(
=( ![]() ,0,﹣1).
,0,﹣1).
設平面DEC的法向量為 ![]() =(x,y,z),
=(x,y,z),
則 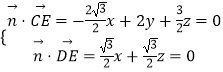 ,令x=
,令x= ![]() ,得
,得 ![]() =(
=( ![]() ,3,﹣1),
,3,﹣1),
設二面角的平面角為θ,
則cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴sinθ= ![]() =
= ![]() ,
,
∴二面角A﹣DE﹣C的正弦值為 ![]()
【解析】(1)解:作SO⊥平面ABCD,連接OB,OA,OD,OB與AD交于點F,連接SF.推導出OB⊥AD,SF⊥AD.從而∠SFB為側面SAD與底面ABCD所成的二面角的平面角,由此能求出點S到平面ABCD的距離.(2)以O為坐標原點,使y軸與BC平行,OB,OS所在直線分別為y軸、z軸建立空間直角坐標系,利用向量法能求出二面角A﹣DE﹣C的正弦值.


科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,若
,若![]() ,
, ![]() 與
與![]() 軸垂直,且
軸垂直,且![]() .
.
(1)求橢圓方程;
(2)過點![]() 且不垂直于坐標軸的直線與橢圓交于
且不垂直于坐標軸的直線與橢圓交于![]() 兩點,已知點
兩點,已知點![]() ,當
,當![]() 時,求滿足
時,求滿足![]() 的直線
的直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別為橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右兩個焦點,橢圓上點M(
=1(a>b>0)的左、右兩個焦點,橢圓上點M( ![]() ,
, ![]() )到F1、F2兩點的距離之和等于4.
)到F1、F2兩點的距離之和等于4.
(1)求橢圓C的方程;
(2)已知過右焦點且垂直于x軸的直線與橢圓交于點N(點N在第一象限),E,F是橢圓C上的兩個動點,如果kEN+KFN=0,證明直線EF的斜率為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】BD是等腰直角三角形△ABC腰AC上的中線,AM⊥BD于點M,延長AM交BC于點N,AF⊥BC于點F,AF與BD交于點E.
(1)求證;△ABE≌△ACN;
(2)求證:∠ADB=∠CDN.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 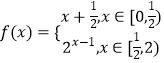 ,若存在x1 , x2 , 當0≤x1<x2<2時,f(x1)=f(x2),則x1f(x2)﹣f(x2)的取值范圍為( )
,若存在x1 , x2 , 當0≤x1<x2<2時,f(x1)=f(x2),則x1f(x2)﹣f(x2)的取值范圍為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面四邊形ABCD內接于圓O,AC是圓O的一條直徑,PA⊥平面ABCD,PA=AC=2,E是PC的中點,∠DAC=∠AOB 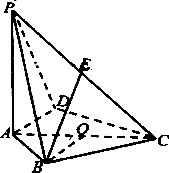
(1)求證:BE∥平面PAD;
(2)若二面角P﹣CD﹣A的正切值為2,求直線PB與平面PCD所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com