
.(本小題滿分l 4分)
如圖,在邊長為4的菱形ABCD中,∠DAB=60°.點(diǎn)E、F分別在邊CD、CB上,點(diǎn)E與點(diǎn)C、D不重合,EF⊥AC,EF∩AC=O.沿EF將△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
(Ⅰ)求證:BD⊥平面POA;
(Ⅱ)當(dāng)PB取得最小值時(shí),請解答以下問題:
(i)求四棱錐P-BDEF的體積;
(ii)若點(diǎn)Q滿足 =λ
=λ (λ
>0),試探究:直線OQ與平面PBD所成角的大小是否一定大于
(λ
>0),試探究:直線OQ與平面PBD所成角的大小是否一定大于 ?并說明理由.
?并說明理由.

(Ⅰ)證明:
∵ 菱形 的對角線互相垂直,
的對角線互相垂直,
∴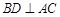 ,∴
,∴ ,······················ 1分
,······················ 1分
∵  ,∴
,∴ .
.
∵ 平面 ⊥平面
⊥平面 ,平面
,平面 平面
平面
 ,
,
且 平面
平面 ,
,
∴  平面
平面 , ······················· 2分
, ······················· 2分
∵  平面
平面 ,
,
∴  .···························· 3分
.···························· 3分
∵  ,
,
∴  平面
平面 . ························· 4分
. ························· 4分
(Ⅱ)如圖,以 為原點(diǎn),建立空間直角坐標(biāo)系
為原點(diǎn),建立空間直角坐標(biāo)系 .··········· 5分
.··········· 5分
(ⅰ)設(shè)
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052519215521874140/SYS201205251923436562624534_DA.files/image021.png">,所以 為等邊三角形,
為等邊三角形,
故 ,
, .
.
又設(shè) ,則
,則 ,
, .
.
所以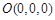 ,
, ,
, ,
,
故  ,··················· 6分
,··················· 6分
所以 ,
,
當(dāng) 時(shí),
時(shí),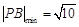 . 此時(shí)
. 此時(shí) ,
, ··········· 7分
··········· 7分
由(Ⅰ)知, 平面
平面
所以 . ······ 8分
. ······ 8分
(ⅱ)設(shè)點(diǎn) 的坐標(biāo)為
的坐標(biāo)為 ,
,
由(i)知, ,則
,則 ,
, ,
, ,
, .
.

所以 ,
,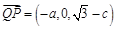 ,·············· 9分
,·············· 9分
∵ ,
,
∴

 .
.
∴ ,
,
∴ . ···· 10分
. ···· 10分
設(shè)平面 的法向量為
的法向量為 ,則
,則 .
.
∵ ,
, ,∴
,∴ ,
,
取 ,解得:
,解得:
 ,
所以
,
所以 . ············· 11分
. ············· 11分
設(shè)直線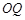 與平面
與平面 所成的角
所成的角 ,
,
∴
 .········ 12分
.········ 12分
又∵ ∴
∴ .······················· 13分
.······················· 13分
∵ ,∴
,∴ .
.
因此直線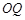 與平面
與平面 所成的角大于
所成的角大于 ,即結(jié)論成立. ········· 14分
,即結(jié)論成立. ········· 14分
【解析】略


 53隨堂測系列答案
53隨堂測系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
|
| x2 |
| 4 |
|
| π |
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區(qū)域內(nèi)作答,若多做,則按作答的前兩題評(píng)分,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
(選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區(qū)域內(nèi)作答,若多做,則按作答的前兩題評(píng)分,解答時(shí)應(yīng)寫出文字說明、證明過程或演算步驟.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 5 |
| π |
| 4 |
| a |
| b |
| c |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:洞口四中數(shù)學(xué)必修2模塊結(jié)業(yè)考試試卷 題型:解答題
19.(本小題滿分8分)已知,過點(diǎn)M(-1,1)的直線l被圓C:x2 + y2-2x + 2y-14 = 0所截得的弦長為4,求直線l的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com