
【題目】若![]() 是遞增數(shù)列,數(shù)列
是遞增數(shù)列,數(shù)列![]() 滿足:對(duì)任意
滿足:對(duì)任意![]() ,存在
,存在![]() ,使得
,使得![]() ,則稱
,則稱![]() 是
是![]() 的“分隔數(shù)列”.
的“分隔數(shù)列”.
(1)設(shè)![]() ,證明:數(shù)列
,證明:數(shù)列![]() 是
是![]() 的分隔數(shù)列;
的分隔數(shù)列;
(2)設(shè)![]() 是
是![]() 的前n項(xiàng)和,
的前n項(xiàng)和,![]() ,判斷數(shù)列
,判斷數(shù)列![]() 是否是數(shù)列
是否是數(shù)列![]() 的分隔數(shù)列,并說(shuō)明理由;
的分隔數(shù)列,并說(shuō)明理由;
(3)設(shè)![]() 是
是![]() 的前n項(xiàng)和,若數(shù)列
的前n項(xiàng)和,若數(shù)列![]() 是
是![]() 的分隔數(shù)列,求實(shí)數(shù)
的分隔數(shù)列,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見(jiàn)解析;(2)數(shù)列![]() 不是數(shù)列
不是數(shù)列![]() 的分隔數(shù)列;(3)
的分隔數(shù)列;(3)![]() .
.
【解析】
(1)由新定義,可得2n≤m+1<2n+2,求得m=2n,即可得證;
(2)運(yùn)用等差數(shù)列的求和公式,結(jié)合新定義,即可判斷;
(3)討論a>0,q>1或a<0,0<q<1,結(jié)合新定義,加以恒成立思想,解不等式即可得到所求范圍.
(1)∵{cn}是遞增數(shù)列,數(shù)列{an}滿足:對(duì)任意n∈N*,存在m∈N*,使得![]() ,
,
∴cn≤am<cn+1,
∵cn=2n,am=m+1,
∴2n≤m+1<2n+2,
∴2n﹣1<m≤2n+1,
∴m=2n,
∴對(duì)任意n∈N*,存在m=2n∈N*,使得![]() ,則稱{an}是{cn}的“分隔數(shù)列;
,則稱{an}是{cn}的“分隔數(shù)列;
(2)cn=n﹣4,Sn是{cn}的前n項(xiàng)和,dn=c3n﹣2,
∴dn=(3n﹣2)﹣4=3n﹣6,
∴d1=﹣3,
∴Sn=![]() =
=![]() n(n﹣7),
n(n﹣7),
若數(shù)列{Sn}是數(shù)列{dn}的分隔數(shù)列,
∴3n﹣6≤![]() m(m﹣7)<3n﹣3,
m(m﹣7)<3n﹣3,
即6(n﹣2)≤m(m﹣7)<6(n﹣1),
由于n=4時(shí),12≤m(m﹣7)<18,
不存在自然數(shù)m,使得不等式成立,
∴數(shù)列{Sn}不是數(shù)列{dn}的分隔數(shù)列;
(3)設(shè)![]() ,Tn是{cn}的前n項(xiàng)和,
,Tn是{cn}的前n項(xiàng)和,
∵數(shù)列{Tn}是{cn}的分隔數(shù)列,
則{cn}為遞增,
當(dāng)a>0時(shí),q>1,
∴aqn﹣1≤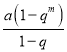 <aqn,
<aqn,
即有qm﹣1<qn(q﹣1),且qm﹣1≥qn﹣1(q﹣1),
當(dāng)1<q<2時(shí),數(shù)列最小項(xiàng)可以得到m不存在;
q>2時(shí),由m=n,qm﹣1≥qn﹣1(q﹣1)成立;
qn﹣1<qn(q﹣1)成立,可得n=2時(shí),q2﹣1<q2(q﹣1),
解得q>2,對(duì)n>3也成立;
當(dāng)a<0時(shí),0<q<1時(shí),
aqn﹣1≤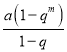 <aqn,
<aqn,
即有1﹣qm>qn(1﹣q),且1﹣qm≤qn﹣1(1﹣q),
取m=n+1,可得1﹣qm>qn(1﹣q)成立,
1﹣qn+1≤qn﹣1(1﹣q)成立,可得q=0恒成立,
則a<0,0<q<1不成立,
綜上可得,a>0,q>2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三梭柱ABC-A1B1C1中,AC=BC,E,F分別為AB,A1B1的中點(diǎn).

(1)求證:AF∥平面B1CE;
(2)若A1B1⊥![]() ,求證:平面B1CE⊥平面ABC.
,求證:平面B1CE⊥平面ABC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() (
(![]() ),其準(zhǔn)線方程
),其準(zhǔn)線方程![]() ,直線
,直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() (
(![]() ),且與拋物線交于
),且與拋物線交于![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),![]() 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(1)求拋物線方程,并注明:![]() 的值與直線
的值與直線![]() 傾斜角的大小無(wú)關(guān);
傾斜角的大小無(wú)關(guān);
(2)若![]() 為拋物線上的動(dòng)點(diǎn),記
為拋物線上的動(dòng)點(diǎn),記![]() 的最小值為函數(shù)
的最小值為函數(shù)![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】私家車的尾氣排放是造成霧霾天氣的重要因素之一,因此在生活中我們應(yīng)該提倡低碳生活,少開(kāi)私家車,盡量選擇綠色出行方式,為預(yù)防霧霾出一份力.為此,很多城市實(shí)施了機(jī)動(dòng)車車尾號(hào)限行,我市某報(bào)社為了解市區(qū)公眾對(duì)“車輛限行”的態(tài)度,隨機(jī)抽查了![]() 人,將調(diào)查情況進(jìn)行整理后制成下表:
人,將調(diào)查情況進(jìn)行整理后制成下表:
年齡(歲) |
|
|
|
|
|
|
頻數(shù) |
|
|
|
|
|
|
贊成人數(shù) |
|
|
|
|
|
|
(![]() )完成被調(diào)查人員的頻率分布直方圖.
)完成被調(diào)查人員的頻率分布直方圖.
(![]() )若從年齡在
)若從年齡在![]() ,
,![]() 的被調(diào)查者中各隨機(jī)選取
的被調(diào)查者中各隨機(jī)選取![]() 人進(jìn)行追蹤調(diào)查,求恰有
人進(jìn)行追蹤調(diào)查,求恰有![]() 人不贊成的概率.
人不贊成的概率.
(![]() )在
)在![]() 在條件下,再記選中的
在條件下,再記選中的![]() 人中不贊成“車輛限行”的人數(shù)為
人中不贊成“車輛限行”的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右頂點(diǎn)分別為
的左、右頂點(diǎn)分別為![]() ,
,![]() ,左、右焦點(diǎn)分別為
,左、右焦點(diǎn)分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 為線段
為線段![]() 的中點(diǎn).
的中點(diǎn).

(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )若過(guò)點(diǎn)
)若過(guò)點(diǎn)![]() 且斜率不為
且斜率不為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),已知直線
兩點(diǎn),已知直線![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,試判斷點(diǎn)
,試判斷點(diǎn)![]() 是否在定直線上?若是,請(qǐng)求出定直線的方程;若不是,請(qǐng)說(shuō)明理由.
是否在定直線上?若是,請(qǐng)求出定直線的方程;若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知△![]() 的內(nèi)角
的內(nèi)角![]() 、
、![]() 、
、![]() 的對(duì)邊分別為
的對(duì)邊分別為![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,且
,且![]() ,延長(zhǎng)線段
,延長(zhǎng)線段![]() 到點(diǎn)
到點(diǎn)![]() ,使得
,使得![]() ,
,![]() .
.
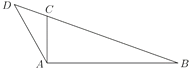
(1)求證:![]() 是直角;
是直角;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() ,命題p:函數(shù)
,命題p:函數(shù)![]() 在
在![]() 內(nèi)單調(diào)遞增;q:函數(shù)
內(nèi)單調(diào)遞增;q:函數(shù)![]() 僅在
僅在![]() 處有極值.
處有極值.
(1)若命題q是真命題,求a的取值范圍;
(2)若命題![]() 是真命題,求a的取值范圍.
是真命題,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)參加![]() 項(xiàng)目生產(chǎn)的工人為
項(xiàng)目生產(chǎn)的工人為![]() 人,平均每人每年創(chuàng)造利潤(rùn)
人,平均每人每年創(chuàng)造利潤(rùn)![]() 萬(wàn)元.根據(jù)現(xiàn)實(shí)的需要,從
萬(wàn)元.根據(jù)現(xiàn)實(shí)的需要,從![]() 項(xiàng)目中調(diào)出
項(xiàng)目中調(diào)出![]() 人參與
人參與![]() 項(xiàng)目的售后服務(wù)工作,每人每年可以創(chuàng)造利潤(rùn)
項(xiàng)目的售后服務(wù)工作,每人每年可以創(chuàng)造利潤(rùn)![]() 萬(wàn)元(
萬(wàn)元(![]() ),
),![]() 項(xiàng)目余下的工人每人每年創(chuàng)造利圖需要提高
項(xiàng)目余下的工人每人每年創(chuàng)造利圖需要提高![]()
(1)若要保證![]() 項(xiàng)目余下的工人創(chuàng)造的年總利潤(rùn)不低于原來(lái)
項(xiàng)目余下的工人創(chuàng)造的年總利潤(rùn)不低于原來(lái)![]() 名工人創(chuàng)造的年總利潤(rùn),則最多調(diào)出多少人參加
名工人創(chuàng)造的年總利潤(rùn),則最多調(diào)出多少人參加![]() 項(xiàng)目從事售后服務(wù)工作?
項(xiàng)目從事售后服務(wù)工作?
(2)在(1)的條件下,當(dāng)從![]() 項(xiàng)目調(diào)出的人數(shù)不能超過(guò)總?cè)藬?shù)的
項(xiàng)目調(diào)出的人數(shù)不能超過(guò)總?cè)藬?shù)的![]() 時(shí),才能使得
時(shí),才能使得![]() 項(xiàng)目中留崗工人創(chuàng)造的年總利潤(rùn)始終不低于調(diào)出的工人所創(chuàng)造的年總利潤(rùn),求實(shí)數(shù)
項(xiàng)目中留崗工人創(chuàng)造的年總利潤(rùn)始終不低于調(diào)出的工人所創(chuàng)造的年總利潤(rùn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
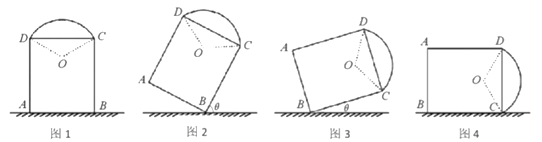
【題目】如圖1,一藝術(shù)拱門由兩部分組成,下部為矩形![]() 的長(zhǎng)分別為
的長(zhǎng)分別為![]() 米和
米和![]() 米,上部是圓心為
米,上部是圓心為![]() 的劣弧
的劣弧![]() ,
,![]()
(1)求圖1中拱門最高點(diǎn)到地面的距離:
(2)現(xiàn)欲以![]() 點(diǎn)為支點(diǎn)將拱門放倒,放倒過(guò)程中矩形
點(diǎn)為支點(diǎn)將拱門放倒,放倒過(guò)程中矩形![]() 所在的平面始終與地面垂直,如圖2、圖3、圖4所示,設(shè)
所在的平面始終與地面垂直,如圖2、圖3、圖4所示,設(shè)![]() 與地面水平線
與地面水平線![]() 所成的角為
所成的角為![]() .若拱門上的點(diǎn)到地面的最大距離恰好為
.若拱門上的點(diǎn)到地面的最大距離恰好為![]() 到地面的距離,試求
到地面的距離,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com