
已知函數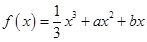
 .
.
(1)若曲線 經過點
經過點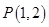 ,曲線
,曲線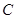 在點
在點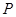 處的切線與直線
處的切線與直線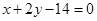 垂直,求
垂直,求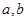 的值;
的值;
(2)在(1)的條件下,試求函數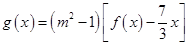 (
(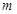 為實常數,
為實常數, )的極大值與極小值之差;
)的極大值與極小值之差;
(3)若 在區間
在區間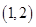 內存在兩個不同的極值點,求證:
內存在兩個不同的極值點,求證: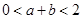 .
.
(1)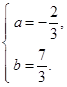
(2)當 或
或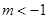 時,
時,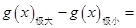
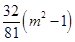 ;
;
當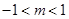 時,
時,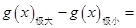
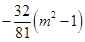 ;
;
(3)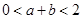 .
.
解析試題分析:(1)利用導數的幾何意義,明確曲線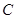 在點
在點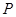 處的切線的斜率為
處的切線的斜率為 ,建立方程
,建立方程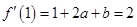 ,再根據曲線
,再根據曲線 經過點
經過點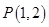 ,得到方程
,得到方程 ,解方程組即得所求.
,解方程組即得所求.
(2)利用“表解法”,確定函數的極值,注意討論 或
或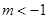 及
及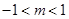 ,的不同情況;
,的不同情況;
(3)根據 在區間
在區間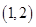 內存在兩個極值點,得到
內存在兩個極值點,得到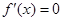 ,
,
即 在
在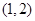 內有兩個不等的實根.
內有兩個不等的實根.
利用二次函數的圖象和性質建立不等式組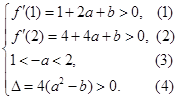 求
求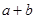 的范圍.
的范圍.
試題解析:(1)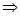
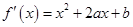 ,
,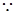 直線
直線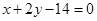 的斜率為
的斜率為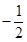 ,
,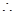 曲線
曲線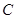 在點
在點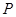 處的切線的斜率為
處的切線的斜率為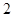 ,
, ①
①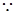 曲線
曲線 經過點
經過點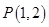 ,
,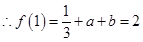 ②
②
由①②得: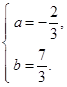 3分
3分
(2)由(1)知: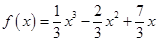 ,
,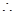
 ,
,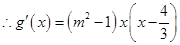 , 由
, 由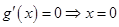 ,或
,或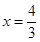 .
.
當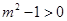 ,即
,即 或
或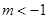 時,
時,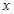 ,
,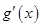 ,
,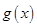 變化如下表
變化如下表