【題目】公差不為零的等差數列{an}中，a3＝7，且a2，a4，a9成等比數列．
(1)求數列{an}的通項公式；
(2)設bn＝
，求數列{bn}的前n項和Sn．
【答案】（1）an＝3n－2；（2）
.
【解析】試題分析：（1）設數列的公差為d，根據a3=7，又a2，a4，a9成等比數列，可得（7+d）2=（7-d）（7+6d），從而可得d=3，進而可求數列{an}的通項公式；
（2）先確定數列{bn}是等比數列，進而可求數列{bn}的前n項和Sn．
試題解析：
(1)由數列{an}為公差不為零的等差數列，設其公差為d，且d≠0.
因為a2，a4，a9成等比數列，
所以a＝a2·a9，即(a1＋3d)2＝(a1＋d)(a1＋8d)，
整理得d2＝3a1d.
因為d≠0，所以d＝3a1.①
因為a3＝7，所以a1＋2d＝7.②
由①②解得a1＝1，d＝3，
所以an＝1＋(n－1)×3＝3n－2.
故數列{an}的通項公式是an＝3n－2.
(2)由(1)知bn＝23n－2，
因為
＝
＝8，
所以{bn}是等比數列，且公比為8，首項b1＝2，
所以Sn＝
＝
.
科目：高中數學 來源： 題型：
【題目】如圖，拋物線
：
與雙曲線
：
（
，
）有公共焦點
，點
是曲線
，
在在第一象限的交點，且
．
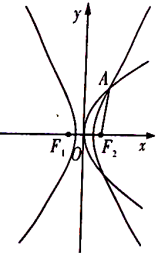
（1）求雙曲線
的方程；
（2）以
為圓心的圓
與雙曲線的一條漸進線相切，圓
．已知點
，過點
作互相垂直分別與圓
、圓
相交的直線
和
，設
被圓
解得的弦長為
，
被圓
截得的弦長為
．試探索
是否為定值？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高二奧賽班N名學生的物理測評成績（滿分120分）分布直方圖如下，已知分數在100～110的學生數有21人。
（Ⅰ）求總人數N和分數在110～115分的人數n;
（Ⅱ）現準備從分數在110～115分的n名學生（女生占
）中任選2人，求其中恰好含有一名女生的概率；
（Ⅲ）為了分析某個學生的學習狀態，對其下一階段的學習提供指導性建議，對他前7次考試的數學成績x（滿分150分），物理成績y進行分析，下面是該生7次考試的成績。
數學 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知該生的物理成績y與數學成績x是線性相關的，若該生的數學成績達到130分，請你估計他的物理成績大約是多少？
附：對于一組數據
其回歸線
的斜率和截距的最小二乘估計分別為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“奶茶妹妹”對某時間段的奶茶銷售量及其價格進行調查，統計出售價
元和銷售量
杯之間的一組數據如下表所示：
價格 | 5 | 5.5 | 6.5 | 7 |
銷售量 | 12 | 10 | 6 | 4 |
通過分析，發現銷售量對奶茶的價格具有線性相關關系．
（Ⅰ）求銷售量對奶茶的價格的回歸直線方程；
（Ⅱ）欲使銷售量為
杯，則價格應定為多少？
附：線性回歸方程為
，其中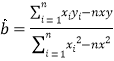
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在銳角△ABC中，三個內角A，B，C所對的邊分別為a，b，c，且acsin C＝(a2＋c2－b2)·sin B．
(1)若C＝
，求A的大小；
(2)若a≠b，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，等邊三角形ABC的邊長為4，M，N分別為AB，AC的中點，沿MN將△AMN折起，使點A到A′的位置．若平面A′MN與平面MNCB垂直，則四棱錐A′MNCB的體積為________．
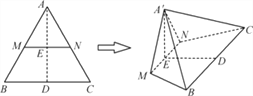
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知：以點
(
)為圓心的圓與
軸交
于點O, A，與y軸交于點O, B，其中O為原點．
（1）求證：△OAB的面積為定值；
（2）設直線
與圓C交于點M, N，若OM = ON，求圓C的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）已知橢圓C的中心在坐標原點，離心率
，且其中一個焦點與拋物線
的焦點重合．(Ⅰ)求橢圓C的方程；(Ⅱ)過點
的動直線l交橢圓C于A、B兩點，試問：在坐標平面上是否存在一個定點T，使得無論l如何轉動，以AB為直徑的圓恒過點T，若存在，求出點T的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
