
【題目】已知非空集合![]() 是由一些函數組成,滿足如下性質:①對任意
是由一些函數組成,滿足如下性質:①對任意![]() ,
,![]() 均存在反函數
均存在反函數![]() ,且
,且![]() ;②對任意
;②對任意![]() ,方程
,方程![]() 均有解;③對任意
均有解;③對任意![]() 、
、![]() ,若函數
,若函數![]() 為定義在
為定義在![]() 上的一次函數,則
上的一次函數,則![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求證:函數
中,求證:函數![]() ;
;
(2)若函數![]() (
(![]() )在集合
)在集合![]() 中,求實數
中,求實數![]() 的取值范圍;
的取值范圍;
(3)若集合![]() 中的函數均為定義在
中的函數均為定義在![]() 上的一次函數,求證:存在一個實數
上的一次函數,求證:存在一個實數![]() ,使得對一切
,使得對一切![]() ,均有
,均有![]() .
.
【答案】(1)見詳解;(2)![]() ;(3)見詳解;
;(3)見詳解;
【解析】
(1)由![]() ,根據性質①可得
,根據性質①可得![]() ,且存在
,且存在![]() ,使得
,使得
![]() ,由
,由![]() ,且為一次函數,根據性質③即可證明.
,且為一次函數,根據性質③即可證明.
(2)由性質②,方程![]() ,即
,即![]() 在
在![]() 上有解,可得
上有解,可得![]() ,
,
變形![]() ,
,![]() .對
.對![]() 與
與![]() 的關系分類討論,利用基本不等式的性質即可求解.
的關系分類討論,利用基本不等式的性質即可求解.
(3)任取![]() ,
,![]() ,由性質①
,由性質①![]() ,不妨設
,不妨設![]() ,
,
(若![]() ,則
,則![]() ,
,![]() ),
),
由性質③函數![]() ,
,
由性質①:![]() ,
,
由性質③:![]()
由性質②方程:![]() ,可得
,可得![]() ,即
,即![]() ,即可得證.
,即可得證.
(1)由![]() ,根據性質①可得
,根據性質①可得![]() ,且存在
,且存在![]() ,使得
,使得
![]() ,由
,由![]() ,且為一次函數,
,且為一次函數,
根據性質③可得:![]() .
.
(2)由性質②,方程![]() ,即
,即![]() 在
在![]() 上有解,
上有解,![]() ,
,
由![]()
![]() ,
,
若![]() ,
,![]() 時,
時,![]() ,且
,且![]() ,
,
![]() 此時
此時![]() 沒有反函數,即不滿足性質①.
沒有反函數,即不滿足性質①.
若![]() ,
,![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 此時
此時![]() 有反函數,
有反函數,
即滿足性質①.
綜上:![]() .
.
(3)任取![]() ,
,![]() ,由性質①
,由性質①![]() ,不妨設
,不妨設![]() ,
,
(若![]() ,則
,則![]() ,
,![]() ),
),
由性質③函數![]() ,
,
由性質①:![]() ,
,
由性質③:![]()
由性質②方程:![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() ,可得
,可得![]() ,
,![]() ,
,
![]() ,可得
,可得![]() ,
,![]() ,
,
由此可知:對于任意兩個函數![]() ,
,![]() ,
,
存在相同的![]() 滿足:
滿足:![]() ,
,
![]() 存在一個實數
存在一個實數![]() ,使得對一切
,使得對一切![]() ,均有
,均有![]() .
.


科目:高中數學 來源: 題型:
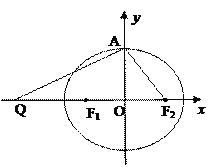
【題目】如圖,設橢圓![]() 的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且
的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且![]() 0,若過 A,Q,F2三點的圓恰好與直線
0,若過 A,Q,F2三點的圓恰好與直線![]() 相切,過定點 M(0,2)的直線
相切,過定點 M(0,2)的直線![]() 與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線
與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線![]() 的斜率
的斜率![]() ,在x軸上是否存在點P(
,在x軸上是否存在點P(![]() ,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出
,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數
的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某氣象站統計了4月份甲、乙兩地的天氣溫度(單位![]() ),統計數據的莖葉圖如圖所示,
),統計數據的莖葉圖如圖所示,
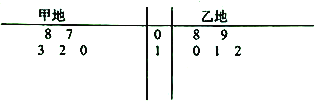
(1)根據所給莖葉圖利用平均值和方差的知識分析甲,乙兩地氣溫的穩定性;
(2)氣象主管部門要從甲、乙兩地各隨機抽取一天的天氣溫度,若甲、乙兩地的溫度之和大于或等于![]() ,則被稱為“甲、乙兩地往來溫度適宜天氣”,求“甲、乙兩地往來溫度適宜天氣”的概率.
,則被稱為“甲、乙兩地往來溫度適宜天氣”,求“甲、乙兩地往來溫度適宜天氣”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
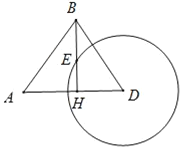
【題目】如圖,我海監船在![]() 島海域例行維權巡航,某時刻航行至
島海域例行維權巡航,某時刻航行至![]() 處,此時測得其北偏東
處,此時測得其北偏東![]() 方向與它相距
方向與它相距![]() 海里的
海里的![]() 處有一外國船只,且
處有一外國船只,且![]() 島位于海監船正東
島位于海監船正東![]() 海里處.
海里處.
(1)求此時該外國船只與![]() 島的距離;
島的距離;
(2)觀測中發現,此外國船只正以每小時![]() 海里的速度沿正南方航行.為了將該船攔截在離
海里的速度沿正南方航行.為了將該船攔截在離![]() 島
島![]() 海里的
海里的![]() 處(
處(![]() 在
在![]() 的正南方向),不讓其進入
的正南方向),不讓其進入![]() 島
島![]() 海里內的海域,試確定海監船的航向,并求其速度的最小值(角度精確到
海里內的海域,試確定海監船的航向,并求其速度的最小值(角度精確到![]() ,速度精確到
,速度精確到![]() 海里/小時).
海里/小時).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若![]() 是定義在
是定義在![]() 上的單調函數,求實數a的取值范圍;
上的單調函數,求實數a的取值范圍;
(2)當![]() 時,判斷
時,判斷![]() 與
與![]() 的圖象在其公共點處是否存在公切線?若存在,求滿足條件的a值的個數;若不存在,請說明理由.
的圖象在其公共點處是否存在公切線?若存在,求滿足條件的a值的個數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四邊形![]() 為正方形,
為正方形,![]() 平面
平面![]() ,四邊形
,四邊形![]() 與四邊形
與四邊形![]() 也都為正方形,連接
也都為正方形,連接![]() ,點
,點![]() 為
為![]() 的中點,有下述四個結論:
的中點,有下述四個結論:
①![]() ; ②
; ②![]() 與
與![]() 所成角為
所成角為![]() ;
;
③![]() 平面
平面![]() ; ④
; ④![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
其中所有正確結論的編號是( )
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】西湖小學為了豐富學生的課余生活開設課后少年宮活動,其中面向二年級的學生共開設了三門課外活動課:七巧板、健美操、剪紙.203班有包括奔奔、果果在內的5位同學報名參加了少年宮活動,每位同學只能挑選一門課外活動課,已知每門課都有人選,則奔奔和果果選擇了同一個課外活動課的選課方法種數為( )
A.18B.36C.72D.144
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com