解:(1)f(x)是奇函數.
證明:∵

=

∴f(x)是R上的奇函數.(3分)
(2)由(1)可知f(x)是奇函數,
當x=0時,f(x)=0,
當x>0且x越來越大,f(x)越來越小,x→+∞,f(x)越來越來→-

,
∴f(x)是R上的減函數.(6分)
(3)∵f(x)是R上的奇函數,
∴f(t
2-2t)>-f(2t
2-k)=f(k-2t
2)(9分)
又f(x)是R上的減函數
∴t
2-2t<k-2t
2即問題等價于對任意t∈[1,2],k>3t
2-2t恒成立(12分)
令g(t)=3t
2-2t,
則g(t)在[1,2]上是增函數,
∴g(t)
max=g(2)=12-4=8(13分)
∴k>8.
分析:(1)利用f(-x)=-f(x)即可作出判斷;
(2)由(1)可知f(x)是奇函數,當x>0且x→+∞,f(x)越來越→-

,可判斷為減函數;
(3)根據題意可將對于任意t∈[1,2],不等式f(t
2-2t)+f(2t
2-k)>0恒成立轉化為“對任意t∈[1,2]k>3t
2-2t恒成立”.再構造函數g(t)=3t
2-2t,利用g(t)在[1,2]上是增函數即可求得k的范圍.
點評:本題考查函數奇偶性與單調性的綜合,著重考查函數奇偶性與單調性的應用,突出考查閉區間上的函數恒成立問題,屬于中檔題.

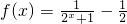 .
. =
=
 ,
, ,可判斷為減函數;
,可判斷為減函數;
