
【題目】(1)已知直線l過點![]() ,它的一個方向向量為
,它的一個方向向量為![]() .
.
①求直線l的方程;
②一組直線![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 都與直線l平行,它們到直線l的距離依次為d,
都與直線l平行,它們到直線l的距離依次為d,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),且直線
),且直線![]() 恰好經過原點,試用n表示d的關系式,并求出直線
恰好經過原點,試用n表示d的關系式,并求出直線![]() 的方程(用n、i表示);
的方程(用n、i表示);
(2)在坐標平面上,是否存在一個含有無窮多條直線![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的直線簇,使它同時滿足以下三個條件:①點
的直線簇,使它同時滿足以下三個條件:①點![]() ;②
;②![]() ,其中
,其中![]() 是直線
是直線![]() 的斜率,
的斜率,![]() 和
和![]() 分別為直線
分別為直線![]() 在x軸和y軸上的截距;③
在x軸和y軸上的截距;③![]()
![]() .
.
【答案】(1)①![]() ;②
;②![]() ,
,![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)根據直線的方向向量可得直線的斜率,結合點斜式即可求得直線方程;根據直線平行且過原點,可得直線![]() 的方程,由平行線間距離公式可得n與d的關系式,設出直線
的方程,由平行線間距離公式可得n與d的關系式,設出直線![]() 的方程,根據點到直線距離公式可求得直線方程.
的方程,根據點到直線距離公式可求得直線方程.
(2)假設存在這樣的直線簇.先求得![]() ,
,![]() 的表達式,進而表示出
的表達式,進而表示出![]() .通過迭加法求得
.通過迭加法求得![]() ,即可證明當
,即可證明當![]() 時,
時,![]() 與
與![]() 不能成立.
不能成立.
(1)①直線l方向向量為![]()
所以直線的斜率為![]()
直線l過點![]() ,由點斜式方程可得
,由點斜式方程可得
![]()
即直線l的方程為:![]() ;
;
②直線![]() 且經過原點,
且經過原點,
![]() 直線
直線![]() 的方程為:
的方程為:![]()
由題意知直線![]() 到l的距離為
到l的距離為![]() ,根據平行線間距離公式可得
,根據平行線間距離公式可得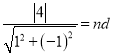
則![]()
設直線![]() 的方程為:
的方程為:![]()
由題意知:直線![]() 到直線l的距離為
到直線l的距離為![]() ,
,
![]()
所以直線![]() 的方程為:
的方程為:![]() ;
;
(2)假設存在滿足題意的直線簇.由①知![]() 的方程為:
的方程為:![]() ,
,![]() ,
,
分別令![]() ,
,![]() 得
得![]() ,
,![]() ,
,
由![]() ,即
,即![]() ,
,![]() ,
,
迭加得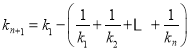 .
.
由③知所有的![]() 同號,僅討論
同號,僅討論![]() 的情形,
的情形,
由![]() ,
,
所以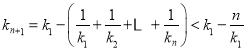
顯然,當![]() 時,
時,![]() 與
與![]() 矛盾!
矛盾!
故滿足題意的直線簇不存在.


 培優三好生系列答案
培優三好生系列答案科目:高中數學 來源: 題型:
【題目】如圖,在長方形ABCD中,AB=2,BC=1,E為DC的中點,F為線段EC(端點除外)上一動點,現將△AFD沿AF折起,使平面ABD⊥平面ABC,則二面角D﹣AF﹣B的平面角余弦值的取值范圍是_____.
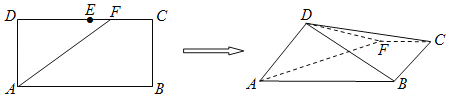
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商店為迎接端午節,推出兩款粽子:花生粽和肉粽.為調查這兩款粽子的受歡迎程度,店員連續10天記錄了這兩種粽子的銷售量,如下表表示(其中銷售單位:個)
天數 銷售量
天數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
花生粽 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 | 100 |
肉粽 | 88 | 97 | 98 | 95 | 101 | 98 | 103 | 106 | 103 | 111 | 100 |
(1)根據兩組數據完成下面莖葉圖:
(2)統計學知識,請評述哪款粽子更受歡迎;
(3)求肉粽銷售量y關于天數t的線性回歸方程,并預估第15天肉粽的銷售量(回歸方程系數精確到0.1)
參考數據:![]() ,參考公式:
,參考公式: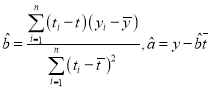
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四邊形ABED中,AB//DE,AB![]() BE,點C在AB上,且AB
BE,點C在AB上,且AB![]() CD,AC=BC=CD=2,現將△ACD沿CD折起,使點A到達點P的位置,且PE
CD,AC=BC=CD=2,現將△ACD沿CD折起,使點A到達點P的位置,且PE![]() .
.
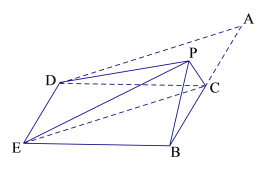
(1)求證:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱錐P-EBC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,側棱
是直角梯形,側棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 為棱
為棱![]() 上的點,
上的點,![]() .
.

(1)若![]() 為棱
為棱![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)當![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是
(1)命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l為直線,![]() ,
,![]() 為兩個不同的平面,若
為兩個不同的平面,若![]() ,
,![]() ,則
,則![]() ;
;
(3)給定命題p,q,若“![]() 為真命題”,則
為真命題”,則![]() 是假命題;
是假命題;
(4)“![]() ”是“
”是“![]() ”的充分不必要條件.
”的充分不必要條件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設不等式![]() 表示的平面區別為
表示的平面區別為![]() .區域
.區域![]() 內的動點
內的動點![]() 到直線
到直線![]() 和直線
和直線![]() 的距離之積為2.記點
的距離之積為2.記點![]() 的軌跡為曲線
的軌跡為曲線![]() .過點
.過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() 垂直于
垂直于![]() 軸,
軸,![]() 為曲線
為曲線![]() 上一點,求
上一點,求![]() 的取值范圍;
的取值范圍;
(3)若以線段![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,求直線
軸相切,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com