【題目】如圖，l1，l2是通過某城市開發區中心O的兩條南北和東西走向的街道，連結M、N兩地之間的鐵路線是圓心在l2上的一段圓弧．若點M在點O正北方向，且|MO|＝3 km，點N到l1，l2的距離分別為4 km和5 km.
(1)建立適當的坐標系，求鐵路線所在圓弧的方程；
(2)若該城市的某中學擬在點O正東方向選址建分校，考慮環境問題，要求校址到點O的距離大于4 km，并且鐵路線上任意一點到校址的距離不能少于
km，求該校址距點O的最近距離．(注：校址視為一個點)
應用題點撥系列答案
狀元及第系列答案
同步奧數系列答案科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出
(百萬元)與銷售額
(百萬元)之間有如下對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果
與
之間具有線性相關關系.
（1）作出這些數據的散點圖；
（2）求這些數據的線性回歸方程
;
（3）預測當廣告費支出為9百萬元時的銷售額。 ( 參考數據： 
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】假設某種設備使用的年限x（年）與所支出的維修費用y（萬元）有以下統計資料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
維修費用y | 2 | 4 | 5 | 6 | 7 |
若由資料知y對x呈線性相關關系。試求：
（1）求
； （2）線性回歸方程
；
（3）估計使用10年時，維修費用是多少？
附：利用“最小二乘法”計算a,b的值時,可根據以下公式：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設點M是棱長為2的正方體的棱AD的中點，P是平面
內一點，若面
分別與面ABCD和面
所成的銳二面角相等，則
長度的最小值是（ ）
A. 
B. 
C. 
D. 1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn=3n﹣1．
（1）求a1 ， a2 ， a3的值；
（2）求數列{an}的通項公式；
（3）求數列{nan}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}的前n項和記為Sn ， a1=1，an+1=2Sn+1（n≥1）．
（1）求{an}的通項公式；
（2）等差數列{bn}的各項為正，其前n項和為Tn ， 且T3=15，又a1+b1 ， a2+b2 ， a3+b3成等比數列，求Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
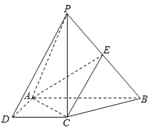
【題目】如圖，在四棱錐
中， 
底面
，底面
是直角梯形， 
， 
， 
， 
是
的中點．
（1）求證：平面
平面
；
（2）若二面角
的余弦值為
，求直線
與平面
所成角的正弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
