
【題目】某商場舉行促銷活動,有兩個摸獎箱,![]() 箱內有一個“
箱內有一個“![]() ”號球、兩個“
”號球、兩個“![]() ”號球、三個“
”號球、三個“![]() ”號球、四個無號球,
”號球、四個無號球,![]() 箱內有五個“
箱內有五個“![]() ”號球、五個“
”號球、五個“![]() ”號球,每次摸獎后放回,消費額滿
”號球,每次摸獎后放回,消費額滿![]() 元有一次
元有一次![]() 箱內摸獎機會,消費額滿
箱內摸獎機會,消費額滿![]() 元有一次
元有一次![]() 箱內摸獎機會,摸得有數字的球則中獎,“
箱內摸獎機會,摸得有數字的球則中獎,“![]() ”號球獎
”號球獎![]() 元、“
元、“![]() ”號球獎
”號球獎![]() 元、“
元、“![]() ”號球獎
”號球獎![]() 元,摸得無號球則沒有獎金.
元,摸得無號球則沒有獎金.
(Ⅰ)經統計,消費額![]() 服從正態分布
服從正態分布![]() ,某天有
,某天有![]() 為顧客,請估計消費額
為顧客,請估計消費額![]() (單位:元)在區間
(單位:元)在區間![]() 內并中獎的人數;
內并中獎的人數;
(Ⅱ)某三位顧客各有一次![]() 箱內摸獎機會,求其中中獎人數
箱內摸獎機會,求其中中獎人數![]() 的分布列;
的分布列;
(Ⅲ)某顧客消費額為![]() 元,有兩種摸獎方法,方法一:三次
元,有兩種摸獎方法,方法一:三次![]() 箱內摸獎機會;方法二:一次
箱內摸獎機會;方法二:一次![]() 箱內摸獎機會,請問:這位顧客選哪一種方法所得獎金的期望值較大.
箱內摸獎機會,請問:這位顧客選哪一種方法所得獎金的期望值較大.
附:若![]() ,則
,則![]()
【答案】(Ⅰ)286;(Ⅱ)答案見解析;(Ⅲ)這位顧客選方法二所得的期望值較大.
【解析】
試題分析:(Ⅰ)依題意得μ=150,σ2=625,得σ=25,100=μ﹣2σ,消費額X在區間(100,150]內的顧客有一次A箱內摸獎機會,中獎率為0.6,人數約為1000×P(μ﹣2σ<X≤μ),可得其中中獎的人數.
(Ⅱ)三位顧客每人一次A箱內摸獎中獎率都為0.6,三人中中獎人數ξ服從二項分布B(3,0.6),![]() ,(k=0,1,2,3),即可得出.
,(k=0,1,2,3),即可得出.
(Ⅲ)利用數學期望的計算公式即可得出.
試題解析:
(Ⅰ)依題意得![]() ,得
,得![]() ,
,
消費額![]() 在區間
在區間![]() 內的顧客有一次
內的顧客有一次![]() 箱內摸獎機會,中獎率為
箱內摸獎機會,中獎率為![]() ,
,
人數約為![]() 人,
人,
其中中獎的人數約為![]() 人,
人,
(Ⅱ)三位顧客每人一次![]() 箱內摸獎中獎率都為
箱內摸獎中獎率都為![]() ,
,
三人中中獎人數![]() 服從二項分布
服從二項分布![]()
故![]() 的分布列為
的分布列為
 (Ⅲ)
(Ⅲ)![]() 箱摸一次所得獎金的期望值為
箱摸一次所得獎金的期望值為![]() ,
,
![]() 想摸一次所得獎金的期望值為
想摸一次所得獎金的期望值為![]() ,
,
方法一所得獎金的期望值為![]() ,方法二所得獎金的期望值為
,方法二所得獎金的期望值為![]() ,
,
所以這位顧客選方法二所得的期望值較大.


科目:高中數學 來源: 題型:
【題目】如圖,一平面與空間四邊形![]() 的對角線
的對角線![]() ,
,![]() 都平行,且交空間四邊形的邊
都平行,且交空間四邊形的邊![]() ,
,![]() ,
,![]() ,
,![]() 分別于
分別于![]() ,
,![]() ,
,![]() ,
,![]() .
.
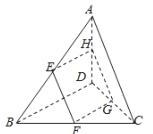
(1)求證:四邊形![]() 為平行四邊形;
為平行四邊形;
(2)若![]() 是邊
是邊![]() 的中點,
的中點,![]() ,
,![]() ,異面直線
,異面直線![]() 與
與![]() 所成的角為60°,求線段
所成的角為60°,求線段![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,
時,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)是否同時存在實數![]() 和正整數
和正整數![]() ,使得函數
,使得函數![]() 在
在![]() 上恰有2019個零點
上恰有2019個零點![]() 若存在,請求出所有符合條件的
若存在,請求出所有符合條件的![]() 和
和![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知矩形的面積為100,則這個矩形的長、寬各為多少時,矩形的周長最短?最短周長是多少?
(2)已知矩形的周長為36,則這個矩形的長、寬各為多少時,它的面積最大?最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
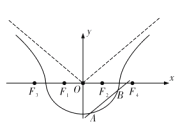
【題目】如圖,曲線![]() 由曲線
由曲線![]() 和曲線
和曲線![]() 組成,其中點
組成,其中點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點,點
所在圓錐曲線的焦點,點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點.
所在圓錐曲線的焦點.
(Ⅰ)若![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(Ⅱ)如圖,作直線![]() 平行于曲線
平行于曲線![]() 的漸近線,交曲線于點
的漸近線,交曲線于點![]() ,求證:弦
,求證:弦![]() 的中點
的中點![]() 必在曲線
必在曲線![]() 的另一條漸進線上;
的另一條漸進線上;
(Ⅲ)對于(Ⅰ)中的曲線![]() ,若直線
,若直線![]() 過點
過點![]() 交曲線
交曲線![]() 于點
于點![]() ,求
,求![]() 與
與![]() 面積之和的最大值.
面積之和的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設雙曲線![]() 的左,右焦點分別為F1,F2,過F1的直線l交雙曲線左支于A,B兩點,則|BF2|+|AF2|的最小值為( )
的左,右焦點分別為F1,F2,過F1的直線l交雙曲線左支于A,B兩點,則|BF2|+|AF2|的最小值為( )
A. ![]() B. 11
B. 11
C. 12 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果△A1B1C1的三個內角的余弦值分別等于△A2B2C2的三個內角的正弦值,則( )
A.△A1B1C1和△A2B2C2都是銳角三角形
B.△A1B1C1和△A2B2C2都是鈍角三角形
C.△A1B1C1是鈍角三角形,△A2B2C2是銳角三角形
D.△A1B1C1是銳角三角形,△A2B2C2是鈍角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com