
【題目】已知函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù))
為自然對數(shù)的底數(shù))
(Ⅰ)試討論函數(shù)![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)![]() 的極值;
的極值;
(Ⅱ)若![]() (
(![]() 為自然對數(shù)的底數(shù)),
為自然對數(shù)的底數(shù)),![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析;(Ⅱ)![]()
【解析】
(Ⅰ)由導(dǎo)數(shù)的求導(dǎo)法則得出![]() ,利用導(dǎo)數(shù)求極值的步驟得出極值。
,利用導(dǎo)數(shù)求極值的步驟得出極值。
(Ⅱ)構(gòu)造函數(shù)令![]() ,求導(dǎo)得到
,求導(dǎo)得到![]() ,利用導(dǎo)數(shù)求最值的方法對
,利用導(dǎo)數(shù)求最值的方法對![]() 的值進行分類討論,即可得出實數(shù)
的值進行分類討論,即可得出實數(shù)![]() 的取值范圍。
的取值范圍。
(Ⅰ)![]() 的定義域為
的定義域為![]() .
.![]() ,
,![]()
當(dāng)![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 單調(diào)遞增,函數(shù)
單調(diào)遞增,函數(shù)![]() 沒有極值.
沒有極值.
當(dāng)![]() 時,由
時,由![]() ,得
,得![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
函數(shù)![]() 的極小值為
的極小值為![]() ,沒有極大值.
,沒有極大值.
(Ⅱ)對![]() ,
,![]() 恒成立,即對
恒成立,即對![]() ,
,![]() ,
,
![]() 對
對![]() ,
,![]() .
.
令![]() ,則
,則![]()
![]() .
.
①當(dāng)![]() ,即
,即![]() 時,對
時,對![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,![]()
![]() ,解得
,解得![]() ,
,![]() 滿足題意.
滿足題意.
![]() 當(dāng)
當(dāng)![]() 時,即
時,即![]() ,對
,對![]() ,
,![]() ,
,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() ,解得
,解得![]()
![]() 滿足題意.
滿足題意.
③當(dāng)![]() ,即
,即![]() 時,對于
時,對于![]() ,
,![]() ;對于
;對于![]() ,
,![]() .
.
![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
![]() .
.
即![]()
設(shè)![]() ,由于
,由于![]() 在
在![]() 單調(diào)遞減,
單調(diào)遞減,
![]()
![]() ,即
,即![]() ,
,
![]() 滿足題意.
滿足題意.
綜上①②③可得,![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:x2+y2+2x﹣4y+3=0.
(1)若直線l:x+y=0與圓C交于A,B兩點,求弦AB的長;
(2)從圓C外一點P(x1,y1)向該圓引一條切線,切點為M,O為坐標(biāo)原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市教育局衛(wèi)生健康所對全市高三年級的學(xué)生身高進行抽樣調(diào)查,隨機抽取了100名學(xué)生,他們身高都處于![]() 五個層次,根據(jù)抽樣結(jié)果得到如下統(tǒng)計圖表,則從圖表中不能得出的信息是( )
五個層次,根據(jù)抽樣結(jié)果得到如下統(tǒng)計圖表,則從圖表中不能得出的信息是( )
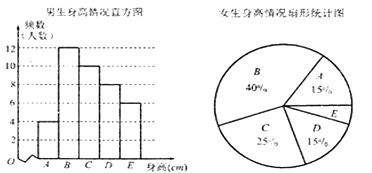
A. 樣本中男生人數(shù)少于女生人數(shù)
B. 樣本中![]() 層次身高人數(shù)最多
層次身高人數(shù)最多
C. 樣本中![]() 層次身高的男生多于女生
層次身高的男生多于女生
D. 樣本中![]() 層次身高的女生有3人
層次身高的女生有3人
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為實常數(shù))
為實常數(shù))
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(3)若存在兩個不相等的正數(shù)![]() 、
、![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,
中,
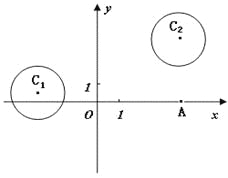
已知圓![]() 和圓
和圓![]() .
.
(1)若直線![]() 過點
過點![]() ,且被圓
,且被圓![]() 截得的弦長為
截得的弦長為![]() ,
,
求直線![]() 的方程;(2)設(shè)P為平面上的點,滿足:
的方程;(2)設(shè)P為平面上的點,滿足:
存在過點P的無窮多對互相垂直的直線![]() 和
和![]() ,
,
它們分別與圓![]() 和圓
和圓![]() 相交,且直線
相交,且直線![]() 被圓
被圓![]()
截得的弦長與直線![]() 被圓
被圓![]() 截得的弦長相等,試求所有滿足條件的點P的坐標(biāo)。
截得的弦長相等,試求所有滿足條件的點P的坐標(biāo)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,直線
,直線![]() (
(![]() )與橢圓
)與橢圓![]() 交于
交于![]() ,
,![]() 兩點(點
兩點(點![]() 在
在![]() 軸的上方).
軸的上方).
(1)若![]() ,求
,求![]() 的面積;
的面積;
(2)是否存在實數(shù)![]() 使得以線段
使得以線段![]() 為直徑的圓恰好經(jīng)過坐標(biāo)原點
為直徑的圓恰好經(jīng)過坐標(biāo)原點![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
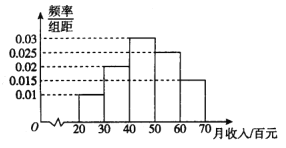
【題目】為了調(diào)查煤礦公司員工的飲食習(xí)慣與月收入之間的關(guān)系,隨機抽取了30名員工,并制作了這30人的月平均收入的頻率分布直方圖和飲食指數(shù)表(說明:圖中飲食指數(shù)低于70的人,飲食以蔬菜為主;飲食指數(shù)高于70的人,飲食以肉類為主).其中月收入4000元以上員工中有11人飲食指數(shù)高于70.
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(Ⅰ)是否有95%的把握認(rèn)為飲食習(xí)慣與月收入有關(guān)系?若有請說明理由,若沒有,說明理由并分析原因;
(Ⅱ)以樣本中的頻率作為概率,從該公司所有主食蔬菜的員工中隨機抽取3人,這3人中月收入4000元以上的人數(shù)為![]() ,求
,求![]() 的分布列與期望;
的分布列與期望;
(Ⅲ)經(jīng)調(diào)查該煤礦公司若干戶家庭的年收入![]() (萬元)和年飲食支出
(萬元)和年飲食支出![]() (萬元)具有線性相關(guān)關(guān)系,并得到
(萬元)具有線性相關(guān)關(guān)系,并得到![]() 關(guān)于
關(guān)于![]() 的回歸直線方程:
的回歸直線方程:![]() .若該公司一個員工與其妻子的月收入恰好都為這30人的月平均收入(該家庭只有兩人收入),估計該家庭的年飲食支出費用.
.若該公司一個員工與其妻子的月收入恰好都為這30人的月平均收入(該家庭只有兩人收入),估計該家庭的年飲食支出費用.
附:
![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com