
【題目】函數f(x)=|2x﹣1|,定義f1(x)=x,fn+1(x)=f(fn(x)),已知函數g(x)=fm(x)﹣x有8個零點,則m的值為( )
A.8
B.4
C.3
D.2
【答案】B
【解析】解:(I)當x∈(﹣∞, ![]() ]時,f2(x)=f(f1(x))=|2x﹣1|=1﹣2x,
]時,f2(x)=f(f1(x))=|2x﹣1|=1﹣2x,
①當x∈(﹣∞, ![]() ]時,f3(x)=|1﹣4x|=1﹣4x,
]時,f3(x)=|1﹣4x|=1﹣4x,
當x∈(﹣∞, ![]() ]時,f4(x)=|1﹣8x|=1﹣8x,
]時,f4(x)=|1﹣8x|=1﹣8x,
此時,g(x)=f4(x)﹣x=1﹣9x,有零點x1= ![]() .
.
當x∈( ![]() ,
, ![]() ]時,f4(x)=|1﹣8x|=8x﹣1,
]時,f4(x)=|1﹣8x|=8x﹣1,
此時,g(x)=f4(x)﹣x=7x﹣1,有零點 ![]() .
.
②當x∈( ![]() ,
, ![]() ]時,f3(x)=|1﹣4x|=4x﹣1,
]時,f3(x)=|1﹣4x|=4x﹣1,
當x∈[ ![]() ,
, ![]() ]時,f4(x)=|8x﹣3|=3﹣8x,
]時,f4(x)=|8x﹣3|=3﹣8x,
此時,g(x)=f4(x)﹣x=3﹣9x,有零點 ![]() .
.
當x∈[ ![]() ,
, ![]() ]時,f4(x)=|8x﹣3|=8x﹣3,
]時,f4(x)=|8x﹣3|=8x﹣3,
此時,g(x)=f4(x)﹣x=7x﹣3,有零點 ![]() ;
;
(II)當x∈( ![]() ,+∞)時,f2(x)=|2x﹣1|=2x﹣1,
,+∞)時,f2(x)=|2x﹣1|=2x﹣1,
③當x∈( ![]() ,
, ![]() ]時,f3(x)=|4x﹣3|=3﹣4x,
]時,f3(x)=|4x﹣3|=3﹣4x,
當x∈( ![]() ,
, ![]() ]時,f4(x)=|5﹣8x|=5﹣8x,
]時,f4(x)=|5﹣8x|=5﹣8x,
此時,g(x)=f4(x)﹣x=5﹣9x,有零點x5= ![]() .
.
當x∈( ![]() ,
, ![]() ]時,f4(x)=|5﹣8x|=8x﹣5,
]時,f4(x)=|5﹣8x|=8x﹣5,
此時,g(x)=f4(x)﹣x=7x﹣5,有零點x6= ![]() .
.
④當x∈( ![]() ,+∞)時,f3(x)=|4x﹣3|=4x﹣3,
,+∞)時,f3(x)=|4x﹣3|=4x﹣3,
當x∈( ![]() ,
, ![]() ]時,f4(x)=|8x﹣7|=7﹣8x,
]時,f4(x)=|8x﹣7|=7﹣8x,
此時,g(x)=f4(x)﹣x=7﹣9x,有零點x7= ![]() .
.
當x∈( ![]() ,+∞)時,f4(x)=|8x﹣7|=8x﹣7,
,+∞)時,f4(x)=|8x﹣7|=8x﹣7,
此時,g(x)=f4(x)﹣x=7x﹣7,有零點x8=1.
綜上所述,若函數g(x)=fm(x)﹣x有8個零點.則m=4.
故選:B.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(ωx+φ)(ω>0,﹣
sin(ωx+φ)(ω>0,﹣ ![]() ≤φ<
≤φ< ![]() ),f(0)=﹣
),f(0)=﹣ ![]() ,且函數f(x)圖象上的任意兩條對稱軸之間距離的最小值是
,且函數f(x)圖象上的任意兩條對稱軸之間距離的最小值是 ![]() .
.
(1)求函數f(x)的解析式;
(2)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求cos(α+
),求cos(α+ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了監控某種零件的一條生產線的生產過程,檢驗員每隔30 min從該生產線上隨機抽取一個零件,并測量其尺寸(單位:cm).下面是檢驗員在一天內依次抽取的16個零件的尺寸:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得![]() ,
, 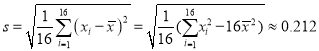 ,
, 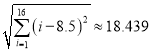 ,
, ![]() ,其中
,其中![]() 為抽取的第
為抽取的第![]() 個零件的尺寸,
個零件的尺寸, ![]() .
.
(1)求![]()
![]() 的相關系數
的相關系數![]() ,并回答是否可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小(若
,并回答是否可以認為這一天生產的零件尺寸不隨生產過程的進行而系統地變大或變小(若![]() ,則可以認為零件的尺寸不隨生產過程的進行而系統地變大或變小).
,則可以認為零件的尺寸不隨生產過程的進行而系統地變大或變小).
(2)一天內抽檢零件中,如果出現了尺寸在![]() 之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
(ⅰ)從這一天抽檢的結果看,是否需對當天的生產過程進行檢查?
(ⅱ)在![]() 之外的數據稱為離群值,試剔除離群值,估計這條生產線當天生產的零件尺寸的均值與標準差.(精確到0.01)
之外的數據稱為離群值,試剔除離群值,估計這條生產線當天生產的零件尺寸的均值與標準差.(精確到0.01)
附:樣本![]()
![]() 的相關系數
的相關系數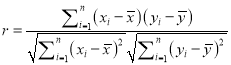 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐中P﹣ABCD,底面ABCD為邊長為 ![]() 的正方形,PA⊥BD.
的正方形,PA⊥BD. 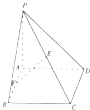
(1)求證:PB=PD;
(2)若E,F分別為PC,AB的中點,EF⊥平面PCD,求直線PB與平面PCD所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于給定的正整數k,若數列{an}滿足![]()
=2kan對任意正整數n(n> k) 總成立,則稱數列{an} 是“P(k)數列”.
(1)證明:等差數列{an}是“P(3)數列”;
若數列{an}既是“P(2)數列”,又是“P(3)數列”,證明:{an}是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上一點,
上一點, ![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
, ![]() 到
到![]() 的準線的距離為
的準線的距離為![]() ,且
,且![]() 的最小值為
的最小值為![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)直線![]() 交
交![]() 于點
于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() ,線段
,線段![]() 的中點分別為
的中點分別為![]() ,若
,若![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:直線
,求證:直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在長方體ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M為B1C1上一點且B1M=2,點N在線段A1D上,A1D⊥AN. 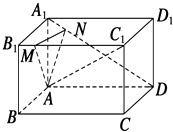
(1)求直線A1D與AM所成角的余弦值;
(2)求直線AD與平面ANM所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中, ![]() 為正三角形,平面
為正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積;
的體積;
(Ⅲ)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,請確定點
?若存在,請確定點![]() 的位置并證明;若不存在,說明理由.
的位置并證明;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com