
【題目】已知數(shù)列{an}的各項均為正數(shù),其前n項的和為Sn , 且對任意的m,n∈N*,
都有(Sm+n+S1)2=4a2ma2n .
(1)求 ![]() 的值;
的值;
(2)求證:{an}為等比數(shù)列;
(3)已知數(shù)列{cn},{dn}滿足|cn|=|dn|=an , p(p≥3)是給定的正整數(shù),數(shù)列{cn},{dn}的前p項的和分別為Tp , Rp , 且Tp=Rp , 求證:對任意正整數(shù)k(1≤k≤p),ck=dk .
【答案】
(1)解:由(Sm+n+S1)2=4a2ma2n.取m=n=1,可得 ![]() ,
,
∵a1,a2>0,∴a2+2a1=2a2,化為 ![]() =2
=2
(2)證明:由(Sm+n+S1)2=4a2ma2n.
令m=n,可得S2n+a1=2a2n,①
∴S2n+2+a1=2a2n+2.②
令m=n+1,可得 ![]() ,③
,③
∴③﹣①可得:a2n+1=2 ![]() ﹣2a2n=
﹣2a2n= ![]()
![]() ,④
,④
②﹣③可得:a2n+2= ![]() ,⑤
,⑤
由④⑤可得: ![]() ,⑥
,⑥
把⑥代入④可得:a2n+1=2a2n,
把⑥代入⑤可得:a2n+2=2a2n+1,
∴ ![]() =2,又
=2,又 ![]() =2.∴
=2.∴ ![]() ,n∈N*.
,n∈N*.
∴{an}為等比數(shù)列,首項為a1,公比為2
(3)證明:由(2)可知:an= ![]() ,
,
∵|cn|=|dn|=an= ![]() ,
,
∴cp=±dp,若cp=﹣dp,
不妨設(shè)cp>0,cp<0,
則Tp≥ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =a1>0,
=a1>0,
Rp≤﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() +
+ ![]() =﹣a1<0,
=﹣a1<0,
這與Tp=Rp矛盾,∴cp=dp,
于是Tp﹣1=Rp﹣1,可得cp﹣1=dp﹣1,于是cp﹣2=dp﹣2,…,c1=d1.
∴對任意正整數(shù)k(1≤k≤p),ck=dk.
【解析】(1)由(Sm+n+S1)2=4a2ma2n . 取m=n=1,可得 ![]() ,利用a1 , a2>0,即可得出.(2)由(Sm+n+S1)2=4a2ma2n . 令m=n,可得S2n+a1=2a2n , S2n+2+a1=2a2n+2 . 令m=n+1,可得
,利用a1 , a2>0,即可得出.(2)由(Sm+n+S1)2=4a2ma2n . 令m=n,可得S2n+a1=2a2n , S2n+2+a1=2a2n+2 . 令m=n+1,可得 ![]() ,化簡整理可得:a2n+1=2a2n , a2n+2=2a2n+1 , 利用等比數(shù)列的通項公式即可得出.(3)由(2)可知:an=
,化簡整理可得:a2n+1=2a2n , a2n+2=2a2n+1 , 利用等比數(shù)列的通項公式即可得出.(3)由(2)可知:an= ![]() ,由于|cn|=|dn|=an=
,由于|cn|=|dn|=an= ![]() ,可得cp=±dp , 若cp=﹣dp , 不妨設(shè)cp>0,cp<0,則Tp≥a1>0,Rp≤﹣a1<0,這與Tp=Rp矛盾,可得cp=dp , 于是Tp﹣1=Rp﹣1 , 即可證明.
,可得cp=±dp , 若cp=﹣dp , 不妨設(shè)cp>0,cp<0,則Tp≥a1>0,Rp≤﹣a1<0,這與Tp=Rp矛盾,可得cp=dp , 于是Tp﹣1=Rp﹣1 , 即可證明.
【考點精析】通過靈活運(yùn)用數(shù)列的前n項和和數(shù)列的通項公式,掌握數(shù)列{an}的前n項和sn與通項an的關(guān)系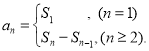 ;如果數(shù)列an的第n項與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項公式即可以解答此題.
;如果數(shù)列an的第n項與n之間的關(guān)系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項公式即可以解答此題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)O為坐標(biāo)原點,曲線x2+y2+2x﹣6y+1=0上有兩點P、Q,滿足關(guān)于直線x+my+4=0對稱,又滿足 ![]() =0.
=0.
(1)求m的值;
(2)求直線PQ的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知線段AB長度為a(a為定值),在其上任意選取一點M,在AB的同一側(cè)分別以AM、MB為底作正方形AMCD、MBEF,⊙P和⊙Q是這兩個正方形的外接圓,它們交于點M、N.試以A為坐標(biāo)原點,建立適當(dāng)?shù)钠矫嬷苯亲鴺?biāo)系. 
(1)證明:不論點M如何選取,直線MN都通過一定點S;
(2)當(dāng) ![]() 時,過A作⊙Q的割線,交⊙Q于G、H兩點,在線段GH上取一點K,使
時,過A作⊙Q的割線,交⊙Q于G、H兩點,在線段GH上取一點K,使 ![]() =
= ![]() 求點K的軌跡.
求點K的軌跡.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知各項均大于1的數(shù)列{an}滿足:a1= ![]() ,an+1=
,an+1= ![]() (an+
(an+ ![]() ),(n∈N*),bn=log5
),(n∈N*),bn=log5 ![]() .
.
(1)證明{bn}為等比數(shù)列,并求{bn}通項公式;
(2)若cn= ![]() ,Tn為{cn}的前n項和,求證:Tn<6.
,Tn為{cn}的前n項和,求證:Tn<6.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下三個關(guān)于圓錐曲線的命題中:
①設(shè)A,B為兩個定點,K為非零常數(shù),若|PA|﹣|PB|=K,則動點P的軌跡是雙曲線.
②方程2x2﹣5x+2=0的兩根可分別作為橢圓和雙曲線的離心率
③雙曲線 ![]() 與橢圓
與橢圓 ![]() +y2=1有相同的焦點.
+y2=1有相同的焦點.
④已知拋物線y2=2px,以過焦點的一條弦AB為直徑作圓,則此圓與準(zhǔn)線相切
其中真命題為(寫出所以真命題的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)雙曲線 ![]() 的離心率e=2,右焦點為F(c,0),方程ax2+bx﹣c=0的兩個實根分別為x1和x2 , 則點P(x1 , x2) 滿足( )
的離心率e=2,右焦點為F(c,0),方程ax2+bx﹣c=0的兩個實根分別為x1和x2 , 則點P(x1 , x2) 滿足( )
A.必在圓x2+y2=2內(nèi)
B.必在圓x2+y2=2外
C.必在圓x2+y2=2上
D.以上三種情形都有可能
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,傾斜角為
,傾斜角為![]() 的直線
的直線![]() 過點
過點![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,
兩點, ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 的面積為
的面積為![]() .
.
(1)求![]() ;
;
(2)設(shè)點![]() 為直線
為直線![]() 與拋物線
與拋物線![]() 在第一象限的交點,過點
在第一象限的交點,過點![]() 作
作![]() 的斜率分別為
的斜率分別為![]() 的兩條弦
的兩條弦![]() ,如果
,如果![]() ,證明直線
,證明直線![]() 過定點,并求出定點坐標(biāo).
過定點,并求出定點坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ]
]
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)設(shè)函數(shù)f(x)= ![]()
![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)調(diào)查了某班全部45名同學(xué)參加書法社團(tuán)和演講社團(tuán)的情況,數(shù)據(jù)如下表:(單位:人)
參加書法社團(tuán) | 未參加書法社團(tuán) | |
參加演講社團(tuán) | 8 | 5 |
未參加演講社團(tuán) | 2 | 30 |
(1)從該班隨機(jī)選1名同學(xué),求該同學(xué)至少參加一個社團(tuán)的概率;
(2)在既參加書法社團(tuán)又參加演講社團(tuán)的8名同學(xué)中,有5名男同學(xué)A1 , A2 , A3 , A4 , A5 , 3名女同學(xué)B1 , B2 , B3 . 現(xiàn)從這5名男同學(xué)和3名女同學(xué)中各隨機(jī)選1人,求A1被選中且B1未被選中的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com