
【題目】在等比數(shù)列{an}中,公比q>1,且滿足a2+a3+a4=28,a3+2是a2與a4的等差中項.
(1)求數(shù)列{an}的通項公式;
(2)若bn=log2an+5 , 且數(shù)列{bn}的前n項的和為Sn , 求數(shù)列{ ![]() }的前n項和Tn .
}的前n項和Tn .
【答案】
(1)解:∵a2+a3+a4=28,∴a1q+a1q2+a1q3=28①;又a3+2是a2、a4的等差中項得到2(a1q2+2)=a1q+a1q3②.
由①得:a1q(1+q+q2)=28③,由②得:a1q2=8,a1q+a1q3=20即a1q(1+q2)=20④
③÷④得 ![]()
∴2q2﹣5q+2=0
∴q=2或q= ![]()
∵q>1,∴q=2
∴數(shù)列{an}的通項公式an=a3qn﹣3=2n;
(2)解:∵an=2n,∴bn=log2 ![]() =n+5,∴b1=6
=n+5,∴b1=6
∴數(shù)列{bn}是以6為首項,1為公差的等差數(shù)列,
∴Sn= ![]()
∴ ![]() =
= ![]()
∴數(shù)列{ ![]() }是以6為首項,
}是以6為首項, ![]() 為公差的等差數(shù)列,
為公差的等差數(shù)列,
∴Tn= ![]() =
= ![]() .
.
【解析】(1)利用a2+a3+a4=28,a3+2是a2與a4的等差中項,建立方程,求出數(shù)列的公比,即可求數(shù)列{an}的通項公式;(2)確定數(shù)列{bn}的通項及前n的和,求得數(shù)列{ ![]() }的通項,即可求和.
}的通項,即可求和.
【考點精析】認真審題,首先需要了解數(shù)列的前n項和(數(shù)列{an}的前n項和sn與通項an的關系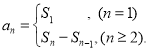 ).
).


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖程序框圖的算法思路,源于我國南宋時期的數(shù)學家秦九韶在他的著作《數(shù)書九章》中提出的秦九韶算法,執(zhí)行該程序框圖,若輸入的n,an , x分別為5,1,﹣2,且a4=5,a3=10,a2=10,a1=5,a0=1,則輸出的v=( ) 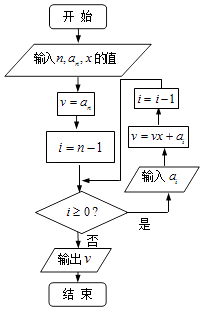
A.1
B.2
C.﹣1
D.﹣2
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知曲線C 的參數(shù)方程為 ![]() (α為參數(shù)),以直角坐標系原點O 為極點,x 軸正半軸為極軸建立極坐標系. (Ⅰ)求曲線C 的極坐標方程;
(α為參數(shù)),以直角坐標系原點O 為極點,x 軸正半軸為極軸建立極坐標系. (Ⅰ)求曲線C 的極坐標方程;
(Ⅱ)設l1:θ= ![]() ,l2:θ=
,l2:θ= ![]() ,若l 1、l2與曲線C 相交于異于原點的兩點 A、B,求△AOB的面積.
,若l 1、l2與曲線C 相交于異于原點的兩點 A、B,求△AOB的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】△ABC中,角A,B,C所對邊分別是a、b、c,且cosA= ![]() .
.
(1)求sin2 ![]() +cos2A的值;
+cos2A的值;
(2)若a= ![]() ,求△ABC面積的最大值.
,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=|x+3|﹣m,m>0,f(x﹣3)≥0的解集為(﹣∞,﹣2]∪[2,+∞). (Ⅰ)求m的值;
(Ⅱ)若x∈R,使得 ![]() 成立,求實數(shù)t的取值范圍.
成立,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù) ![]() ,為了得到函數(shù)g(x)=sin2x的圖象,則只需將f(x)的圖象( )
,為了得到函數(shù)g(x)=sin2x的圖象,則只需將f(x)的圖象( )
A.向右平移 ![]() 個長度單位
個長度單位
B.向右平移 ![]() 個長度單位
個長度單位
C.向左平移 ![]() 個長度單位
個長度單位
D.向左平移 ![]() 個長度單位
個長度單位
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知曲線C1的極坐標方程為ρ=6cosθ,曲線C2的極坐標方程為θ= ![]() (p∈R),曲線C1 , C2相交于A,B兩點. (Ⅰ)把曲線C1 , C2的極坐標方程轉(zhuǎn)化為直角坐標方程;
(p∈R),曲線C1 , C2相交于A,B兩點. (Ⅰ)把曲線C1 , C2的極坐標方程轉(zhuǎn)化為直角坐標方程;
(Ⅱ)求弦AB的長度.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() sin2x﹣2cos2x﹣1,x∈R.
sin2x﹣2cos2x﹣1,x∈R.
(Ⅰ)求函數(shù)f(x)的最小正周期和最小值;
(Ⅱ)在△ABC中,A,B,C的對邊分別為a,b,c,已知c= ![]() ,f(C)=0,sinB=2sinA,求a,b的值.
,f(C)=0,sinB=2sinA,求a,b的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com