
【題目】已知直線l:y=﹣x+1與橢圓C: ![]() =1(a>b>0))相交于不同的兩點(diǎn)A、B,且線段AB的中點(diǎn)P的坐標(biāo)為(
=1(a>b>0))相交于不同的兩點(diǎn)A、B,且線段AB的中點(diǎn)P的坐標(biāo)為( ![]() ,
, ![]() )
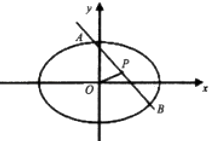
) 
(1)求橢圓C離心率;
(2)設(shè)O為坐標(biāo)原點(diǎn),且2|OP|=|AB|,求橢圓C的方程.
【答案】
(1)解:將直線y=1﹣x代入橢圓方程,可得
(b2+a2)x2﹣2a2x+a2﹣a2b2=0,
則x1+x2= ![]() ,
,
由AB的中點(diǎn)P的坐標(biāo)為( ![]() ,
, ![]() ),可得
),可得
![]() =
= ![]() ,即為a2=2b2,
,即為a2=2b2,
可得c2=a2﹣b2= ![]() a2,
a2,
則橢圓C離心率為e= ![]() =
= ![]()
(2)解:由(1)可得,
△=4a4﹣4(b2+a2)(a2﹣a2b2)>0,
可得a2+b2>1,即b2> ![]() ,
,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() =
= ![]() ,
,
由2|OP|=|AB|,可得:
2 ![]() =
= ![]()
![]() ,
,
解得b2= ![]() (滿足△>0),即有a2=
(滿足△>0),即有a2= ![]() ,
,
可得橢圓方程為 ![]() =1
=1
【解析】(1)將直線方程代入橢圓方程,運(yùn)用韋達(dá)定理和中點(diǎn)坐標(biāo)公式,結(jié)合離心率公式計算即可得到所求值;(2)運(yùn)用韋達(dá)定理和弦長公式,以及兩點(diǎn)的距離公式,解方程即可得到a,b,進(jìn)而得到橢圓方程.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市自來水公司每兩個月(記為一個收費(fèi)周期)對用戶收一次水費(fèi),收費(fèi)標(biāo)準(zhǔn)如下:當(dāng)每戶用水量不超過![]() 噸時,按每噸
噸時,按每噸![]() 元收取;當(dāng)該用戶用水量超過
元收取;當(dāng)該用戶用水量超過![]() 噸時,超出部分按每噸
噸時,超出部分按每噸![]() 元收取.
元收取.
(1)記某用戶在一個收費(fèi)周期的用水量為![]() 噸,所繳水費(fèi)為
噸,所繳水費(fèi)為![]() 元,寫出
元,寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式.
的函數(shù)解析式.
(2)在某一個收費(fèi)周期內(nèi),若甲、乙兩用戶所繳水費(fèi)的和為![]() 元,且甲、乙兩用戶用水量之比為
元,且甲、乙兩用戶用水量之比為![]() ,試求出甲、乙兩用戶在該收費(fèi)周期內(nèi)各自的用水量和水費(fèi).
,試求出甲、乙兩用戶在該收費(fèi)周期內(nèi)各自的用水量和水費(fèi).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體ABCD – A1B1C1D1中,點(diǎn)E,F,G分別是棱BC,A1B1,B1C1的中點(diǎn).
(1)求異面直線EF與DG所成角的余弦值;
(2)設(shè)二面角A—BD—G的大小為θ,求 |cosθ| 的值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,左右焦點(diǎn)分別為
,左右焦點(diǎn)分別為![]() 和
和![]() ,以點(diǎn)
,以點(diǎn)![]() 為圓心,以
為圓心,以![]() 為半徑的圓與以點(diǎn)
為半徑的圓與以點(diǎn)![]() 為圓心,以
為圓心,以![]() 為半徑的圓相交,且交點(diǎn)在橢圓
為半徑的圓相交,且交點(diǎn)在橢圓![]() 上.
上.
(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )設(shè)橢圓
)設(shè)橢圓![]() ,
, ![]() 為橢圓
為橢圓![]() 上任意一點(diǎn),過點(diǎn)
上任意一點(diǎn),過點(diǎn)![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點(diǎn),射線
兩點(diǎn),射線![]() 交橢圓
交橢圓![]() 于點(diǎn)
于點(diǎn)![]() .
.
①求![]() 的值.
的值.
②(理科生做)求![]() 面積的最大值.
面積的最大值.
③(文科生做)當(dāng)![]() 時,
時, ![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法中不正確的序號為____________.
①若函數(shù)![]() 在
在![]() 上單調(diào)遞減,則實(shí)數(shù)
上單調(diào)遞減,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() ;
;
②函數(shù)![]() 是偶函數(shù),但不是奇函數(shù);
是偶函數(shù),但不是奇函數(shù);
③已知函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,則函數(shù)
,則函數(shù)![]() 的定義域是
的定義域是![]() ;
;
④若函數(shù)![]() 在
在![]() 上有最小值-4,(
上有最小值-4,(![]() ,
,![]() 為非零常數(shù)),則函數(shù)
為非零常數(shù)),則函數(shù)![]() 在
在![]() 上有最大值6.
上有最大值6.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)一天中不同時刻的用電量![]() (萬千瓦時)關(guān)于時間
(萬千瓦時)關(guān)于時間![]() (小時,
(小時,![]() )的函數(shù)
)的函數(shù)![]() 近似滿足
近似滿足![]() ,如圖是函數(shù)
,如圖是函數(shù)![]() 的部分圖象(
的部分圖象(![]() 對應(yīng)凌晨
對應(yīng)凌晨![]() 點(diǎn)).
點(diǎn)).

(Ⅰ)根據(jù)圖象,求![]() 的值;
的值;
(Ⅱ)由于當(dāng)?shù)囟眷F霾嚴(yán)重,從環(huán)保的角度,既要控制火力發(fā)電廠的排放量,電力供應(yīng)有限;又要控制企業(yè)的排放量,于是需要對各企業(yè)實(shí)行分時拉閘限電措施.已知該企業(yè)某日前半日能分配到的供電量![]() (萬千瓦時)與時間
(萬千瓦時)與時間![]() (小時)的關(guān)系可用線性函數(shù)模型
(小時)的關(guān)系可用線性函數(shù)模型![]() 模擬.當(dāng)供電量小于該企業(yè)的用電量時,企業(yè)就必須停產(chǎn).初步預(yù)計停產(chǎn)時間在中午11點(diǎn)到12點(diǎn)間,為保證該企業(yè)既可提前準(zhǔn)備應(yīng)對停產(chǎn),又可盡量減少停產(chǎn)時間,請從這個初步預(yù)計的時間段開始,用二分法幫其估算出精確到15分鐘的停產(chǎn)時間段.
模擬.當(dāng)供電量小于該企業(yè)的用電量時,企業(yè)就必須停產(chǎn).初步預(yù)計停產(chǎn)時間在中午11點(diǎn)到12點(diǎn)間,為保證該企業(yè)既可提前準(zhǔn)備應(yīng)對停產(chǎn),又可盡量減少停產(chǎn)時間,請從這個初步預(yù)計的時間段開始,用二分法幫其估算出精確到15分鐘的停產(chǎn)時間段.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 是實(shí)數(shù)集
是實(shí)數(shù)集![]() 上的奇函數(shù),求
上的奇函數(shù),求![]() 的值;
的值;
(2)用定義證明![]() 在實(shí)數(shù)集
在實(shí)數(shù)集![]() 上的單調(diào)遞增;
上的單調(diào)遞增;
(3)若![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ,且[
,且[![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 。
。
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(2)若函數(shù)![]() 在
在![]() 處有極小值,求實(shí)數(shù)
處有極小值,求實(shí)數(shù)![]() 的值。
的值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,則實(shí)數(shù)
上單調(diào)遞減,則實(shí)數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】∵![]() ,
,
∴![]() ,
,
由![]() 得
得![]() ,
,
∴函數(shù)![]() 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為![]() ,
,
又函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴![]()
![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .選C.
.選C.
點(diǎn)睛:已知函數(shù)在區(qū)間上的單調(diào)性求參數(shù)的方法
(1)利用導(dǎo)數(shù)求解,轉(zhuǎn)化為導(dǎo)函數(shù)在該區(qū)間上大于等于零(或小于等于零)恒成立的問題求解,一般通過分離參數(shù)化為求函數(shù)的最值的問題.
(2)先求出已知函數(shù)的單調(diào)區(qū)間,然后將問題轉(zhuǎn)化為所給的區(qū)間是函數(shù)相應(yīng)的單調(diào)區(qū)間的子集的問題處理.
【題型】單選題
【結(jié)束】
7
【題目】設(shè)![]() ,函數(shù)
,函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后與原圖象重合,則
個單位長度后與原圖象重合,則![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com