
【題目】對于函數f(x),若存在區間A=[m,n],使得{y|y=f(x),x∈A}=A,則稱函數f(x)為“可等域函數”,區間A為函數f(x)的一個“可等域區間”.給出下列四個函數: ①f(x)=sin ![]() x;②f(x)=2x2﹣1;③f(x)=|1﹣2x|
x;②f(x)=2x2﹣1;③f(x)=|1﹣2x|
其中存在“可等域區間”的“可等域函數”為( )
A.①
B.②
C.①②
D.①②③
【答案】D
【解析】解:①f(x)=sin ![]() x的可等域區間有[0,1];②f(x)=2x2﹣1的可等域區間有[﹣1,1];③f(x)=|1﹣2x|的可等域區間有[0,1].
x的可等域區間有[0,1];②f(x)=2x2﹣1的可等域區間有[﹣1,1];③f(x)=|1﹣2x|的可等域區間有[0,1].
故選:D.
【考點精析】認真審題,首先需要了解函數的定義域及其求法(求函數的定義域時,一般遵循以下原則:①![]() 是整式時,定義域是全體實數;②
是整式時,定義域是全體實數;②![]() 是分式函數時,定義域是使分母不為零的一切實數;③
是分式函數時,定義域是使分母不為零的一切實數;③![]() 是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零),還要掌握函數的值域(求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的)的相關知識才是答題的關鍵.
是偶次根式時,定義域是使被開方式為非負值時的實數的集合;④對數函數的真數大于零,當對數或指數函數的底數中含變量時,底數須大于零且不等于1,零(負)指數冪的底數不能為零),還要掌握函數的值域(求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的)的相關知識才是答題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD和BCEG均為直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE= ![]() ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2. 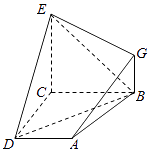
(1)證明:AG∥平面BDE.
(2)求平面BDE和平面ADE所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出了四個類比推理: ①由“若a,b,c∈R則(ab)c=a(bc)”類比推出“若a,b,c為三個向量則( ![]()
![]() )
) ![]() =
= ![]() (
( ![]()
![]() )”;
)”;
②“a,b為實數,若a2+b2=0則a=b=0”類比推出“z1 , z2為復數,若 ![]() ”;
”;
③“在平面內,三角形的兩邊之和大于第三邊”類比推出“在空間中,四面體的任意三個面的面積之和大于第四個面的面積”;
④“在平面內,過不在同一條直線上的三個點有且只有一個圓”類比推出“在空間中,過不在同一個平面上的四個點有且只有一個球”.
上述四個推理中,結論正確的個數有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知sin(A+C)=8sin2 ![]() .
.
(1)求cosB;
(2)若a+c=6,△ABC的面積為2,求b.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,函數f(x)=2cosxsin(x﹣A)+sinA(x∈R)在x= ![]() 處取得最大值.
處取得最大值.
(1)當 ![]() 時,求函數f(x)的值域;
時,求函數f(x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校對高一年級學生的數學成績進行統計,全年級同學的成績全部介于60分與100分之間,將他們的成績數據繪制如圖所示的頻率分布直方圖.現從全體學生中,采用分層抽樣的方法抽取80名同學的試卷進行分析,則從成績在[80,100]內的學生中抽取的人數為( )
A.56
B.32
C.24
D.18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知0<a<1,函數f(x)=logax.
(1)若f(5a﹣1)≥f(2a),求實數a的最大值;
(2)當a= ![]() 時,設g(x)=f(x)﹣3x+2m,若函數g(x)在(1,2)上有零點,求實數m的取值范圍.
時,設g(x)=f(x)﹣3x+2m,若函數g(x)在(1,2)上有零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省高考改革新方案,不分文理科,高考成績實行“3+3”的構成模式,第一個“3”是語文、數學、外語,每門滿分150分,第二個“3”由考生在思想政治、歷史、地理、物理、化學、生物6個科目中自主選擇其中3個科目參加等級性考試,每門滿分100分,高考錄取成績卷面總分滿分750分.為了調查學生對物理、化學、生物的選考情況,將“某市某一屆學生在物理、化學、生物三個科目中至少選考一科的學生”記作學生群體S,從學生群體S中隨機抽取了50名學生進行調查,他們選考物理,化學,生物的科目數及人數統計如表:
選考物理、化學、生物的科目數 | 1 | 2 | 3 |
人數 | 5 | 25 | 20 |
(I)從所調查的50名學生中任選2名,求他們選考物理、化學、生物科目數量不相等的概率;
(II)從所調查的50名學生中任選2名,記X表示這2名學生選考物理、化學、生物的科目數量之差的絕對值,求隨機變量X的分布列和數學期望;
(III)將頻率視為概率,現從學生群體S中隨機抽取4名學生,記其中恰好選考物理、化學、生物中的兩科目的學生數記作Y,求事件“y≥2”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com