
【題目】若數(shù)列{an}的前n項(xiàng)和為Sn , 滿足a1=1,Sn=an+1+n,則其通項(xiàng)公式為 .
【答案】![]()
【解析】解:由Sn=an+1+n,得Sn﹣1=an+n﹣1(n≥2),
兩式作差得:an=an+1﹣an+1,即an+1=2an﹣1,
∴an+1﹣1=2(an﹣1)(n≥2),
由a1=1,Sn=an+1+n,得a2=0,
a2﹣1=﹣1,a1﹣1=0,不滿足an+1﹣1=2(an﹣1),
∴數(shù)列{an﹣1}自第二項(xiàng)起構(gòu)成以2為公比的等比數(shù)列,
∴ ![]() ,即
,即 ![]() (n≥2).
(n≥2).
∴ ![]() .
.
所以答案是: ![]() .
.
【考點(diǎn)精析】本題主要考查了數(shù)列的通項(xiàng)公式的相關(guān)知識(shí)點(diǎn),需要掌握如果數(shù)列an的第n項(xiàng)與n之間的關(guān)系可以用一個(gè)公式表示,那么這個(gè)公式就叫這個(gè)數(shù)列的通項(xiàng)公式才能正確解答此題.


 補(bǔ)充習(xí)題江蘇系列答案
補(bǔ)充習(xí)題江蘇系列答案 學(xué)練快車(chē)道口算心算速算天天練系列答案
學(xué)練快車(chē)道口算心算速算天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某班同學(xué)準(zhǔn)備參加學(xué)校在寒假里組織的“社區(qū)服務(wù)”、“進(jìn)敬老院”、“參觀工廠”、“民俗調(diào)查”、“環(huán)保宣傳”五個(gè)項(xiàng)目的社會(huì)實(shí)踐活動(dòng),每天只安排一項(xiàng)活動(dòng),并要求在周一至周五內(nèi)完成.其中“參觀工廠”與“環(huán)保宣講”兩項(xiàng)活動(dòng)必須安排在相鄰兩天,“民俗調(diào)查”活動(dòng)不能安排在周一.則不同安排方法的種數(shù)是( )
A.48 B.24 C.36 D.64
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)雙曲線 ![]() =1(a>0,b>0)的右焦點(diǎn)為F,右頂點(diǎn)為A,過(guò)F作AF的垂線與雙曲線的兩條漸近線交于B、C兩點(diǎn),過(guò)B、C分別作AC、AB的垂線,兩垂線交于點(diǎn)D.若D到直線BC的距離小于2(a+
=1(a>0,b>0)的右焦點(diǎn)為F,右頂點(diǎn)為A,過(guò)F作AF的垂線與雙曲線的兩條漸近線交于B、C兩點(diǎn),過(guò)B、C分別作AC、AB的垂線,兩垂線交于點(diǎn)D.若D到直線BC的距離小于2(a+ ![]() ),則該雙曲線的離心率的取值范圍是( )
),則該雙曲線的離心率的取值范圍是( )
A.(1,2)
B.( ![]() ,2)
,2)
C.(1, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿分14分)如圖,四棱錐![]() 的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點(diǎn),連結(jié)
的中點(diǎn),連結(jié)![]() .求證:
.求證:
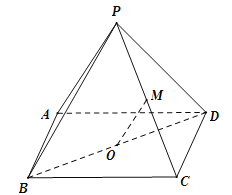
(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知p:關(guān)于x的方程ax2+2x+1=0至少有一個(gè)負(fù)根,q:a≤1,則¬p是¬q的( )
A.充要條件
B.充分不必要條件
C.必要不充分條件
D.不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an}的前n項(xiàng)和為Sn , 且滿足an+2SnSn﹣1=0(n≥2),a1= ![]() .
.
(1)求證:{ ![]() }是等差數(shù)列;
}是等差數(shù)列;
(2)求an的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(本小題滿分14分)如圖,四棱錐![]() 的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn),連結(jié)
的中點(diǎn),連結(jié)![]() .求證:
.求證:

(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】航空測(cè)量組的飛機(jī)航線和山頂在同一鉛直平面內(nèi),已知飛機(jī)的高度為海拔10000m,速度為180km(千米)/h(小時(shí)),飛機(jī)先看到山頂?shù)母┙菫?5°,經(jīng)過(guò)420s(秒)后又看到山頂?shù)母┙菫?5°,求山頂?shù)暮0胃叨龋ㄈ?![]() ,
, ![]() ).
). 
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,當(dāng)∠x(chóng)Oy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)時(shí),定義平面坐標(biāo)系xOy為α﹣仿射坐標(biāo)系.在α﹣仿射坐標(biāo)系中,任意一點(diǎn)P的斜坐標(biāo)這樣定義:
,π)時(shí),定義平面坐標(biāo)系xOy為α﹣仿射坐標(biāo)系.在α﹣仿射坐標(biāo)系中,任意一點(diǎn)P的斜坐標(biāo)這樣定義: ![]() 、
、 ![]() 分別為與x軸、y軸正向相同的單位向量,若
分別為與x軸、y軸正向相同的單位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,則記為
,則記為 ![]() =(x,y).現(xiàn)給出以下說(shuō)法:
=(x,y).現(xiàn)給出以下說(shuō)法:
①在α﹣仿射坐標(biāo)系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,則t=6;
,則t=6;
②在α﹣仿射坐標(biāo)系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),則
),則 ![]()
![]() =0;
=0;
③在60°﹣仿射坐標(biāo)系中,若P(2,﹣1),則| ![]() |=
|= ![]() ;
;
其中說(shuō)法正確的有 . (填出所有說(shuō)法正確的序號(hào))
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com