
【題目】如圖,一架飛機(jī)以600km/h的速度,沿方位角60°的航向從A地出發(fā)向B地飛行,飛行了36min后到達(dá)E地,飛機(jī)由于天氣原因按命令改飛C地,已知AD=600 ![]() km,CD=1200km,BC=500km,且∠ADC=30°,∠BCD=113°.問收到命令時(shí)飛機(jī)應(yīng)該沿什么航向飛行,此時(shí)E地離C地的距離是多少?(參考數(shù)據(jù):tan37°=
km,CD=1200km,BC=500km,且∠ADC=30°,∠BCD=113°.問收到命令時(shí)飛機(jī)應(yīng)該沿什么航向飛行,此時(shí)E地離C地的距離是多少?(參考數(shù)據(jù):tan37°= ![]() )
) 
【答案】解:連接AC,CE,在△ACD中由余弦定理,得: ![]() ,
,
∴AC=600,
則CD2=AD2+AC2 , 即△ACD是直角三角形,且∠ACD=60°,
又∠BCD=113°,則∠ACB=53°,
∵tan37°= ![]() ,
,
∴cos53°=sin37°= ![]() .
.
在△ABC中,由余弦定理,得: ![]() ,則AB=500,
,則AB=500,
又BC=500,則△ABC是等腰三角形,且∠BAC=53°,
由已知有 ![]() ,
,
在△ACE中,由余弦定理,有 ![]() ,
,
又AC2=AE2+CE2 , 則∠AEC=90°.
由飛機(jī)出發(fā)時(shí)的方位角為600 , 則飛機(jī)由E地改飛C地的方位角為:90°+60°=150°.
答:收到命令時(shí)飛機(jī)應(yīng)該沿方位角150°的航向飛行,E地離C地480km.
【解析】在△ACD中使用余弦定理得出AC及∠ACD,在△ABC中使用余弦定理得出AB及∠CAE,再在△ACE中使用余弦定理得出CE及∠AEC.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若m個(gè)不全相等的正數(shù)a1 , a2 , …am依次圍成一個(gè)圓圈使每個(gè)ak(1≤k≤m,k∈N)都是其左右相鄰兩個(gè)數(shù)平方的等比中項(xiàng),則正整數(shù)m的最小值是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4—4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中曲線
中曲線![]() 經(jīng)伸縮變換
經(jīng)伸縮變換![]() 后得到曲線
后得到曲線![]() ,在以
,在以![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸的正半軸為極軸的極坐標(biāo)系中,曲線
軸的正半軸為極軸的極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的參數(shù)方程和
的參數(shù)方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)![]() 為曲線
為曲線![]() 上的一點(diǎn),又
上的一點(diǎn),又![]() 向曲線
向曲線![]() 引切線,切點(diǎn)為
引切線,切點(diǎn)為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求證: ![]() 與
與 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 與
與 ![]() ﹣k
﹣k ![]() 的長度相等,求β﹣α的值(k為非零的常數(shù)).
的長度相等,求β﹣α的值(k為非零的常數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為推行“新課堂”教學(xué)法,某化學(xué)老師分別用傳統(tǒng)教學(xué)和“新課堂”兩種不同的教學(xué)方式,在甲、乙兩個(gè)平行班進(jìn)行教學(xué)實(shí)驗(yàn),為了解教學(xué)效果,期中考試后,分別從兩個(gè)班級中各隨機(jī)抽取![]() 名學(xué)生的成績進(jìn)行統(tǒng)計(jì),作出的莖葉圖如下圖,記成績不低于
名學(xué)生的成績進(jìn)行統(tǒng)計(jì),作出的莖葉圖如下圖,記成績不低于![]() 分者為“成績優(yōu)良”.
分者為“成績優(yōu)良”.

(1)分別計(jì)算甲、乙兩班![]() 個(gè)樣本中,化學(xué)分?jǐn)?shù)前十的平均分,并據(jù)此判斷哪種教學(xué)方式的教學(xué)效果更
個(gè)樣本中,化學(xué)分?jǐn)?shù)前十的平均分,并據(jù)此判斷哪種教學(xué)方式的教學(xué)效果更
佳;
(2)甲、乙兩班![]() 個(gè)樣本中,成績在
個(gè)樣本中,成績在![]() 分以下(不含
分以下(不含![]() 分)的學(xué)生中任意選取
分)的學(xué)生中任意選取![]() 人,求這
人,求這![]() 人來自不同班級的概率;
人來自不同班級的概率;
(3)由以上統(tǒng)計(jì)數(shù)據(jù)填寫下面![]() 列聯(lián)表,并判斷能否在犯錯(cuò)誤的概率不超過
列聯(lián)表,并判斷能否在犯錯(cuò)誤的概率不超過![]() 的前提下認(rèn)為“成績優(yōu)良與教學(xué)方式有關(guān)”?
的前提下認(rèn)為“成績優(yōu)良與教學(xué)方式有關(guān)”?
甲班 | 乙班 | 總計(jì) | |
成績優(yōu)良 | |||
成績不優(yōu)良 | |||
總計(jì) |
附: 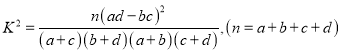
獨(dú)立性檢驗(yàn)臨界值表:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的兩個(gè)焦點(diǎn)坐標(biāo)分別是
的兩個(gè)焦點(diǎn)坐標(biāo)分別是![]() ,并且經(jīng)過
,并且經(jīng)過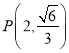 .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過橢圓![]() 的右焦點(diǎn)
的右焦點(diǎn)![]() 作直線
作直線![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點(diǎn),當(dāng)
兩點(diǎn),當(dāng)![]() 的面積最大時(shí),求直線
的面積最大時(shí),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(文科)已知的橢圓![]() 的左、右兩個(gè)焦點(diǎn)分別為
的左、右兩個(gè)焦點(diǎn)分別為![]() ,上頂點(diǎn)
,上頂點(diǎn)![]() ,
, ![]() 是正三角形且周長為6.
是正三角形且周長為6.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程及離心率;
的標(biāo)準(zhǔn)方程及離心率;
(2) ![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn), ![]() 是直線
是直線![]() 上的一個(gè)動(dòng)點(diǎn),求
上的一個(gè)動(dòng)點(diǎn),求![]() 的最小值,并求出此時(shí)點(diǎn)
的最小值,并求出此時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
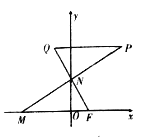
【題目】已知點(diǎn)![]() ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)![]() ,
, ![]() 分別在
分別在![]() 軸,
軸, ![]() 軸上運(yùn)動(dòng),
軸上運(yùn)動(dòng), ![]() ,
, ![]() 為平面上一點(diǎn),
為平面上一點(diǎn), ![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 平行于
平行于![]() 軸交
軸交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() .
.
(Ⅰ)求點(diǎn)![]() 的軌跡曲線
的軌跡曲線![]() 的方程;
的方程;
(Ⅱ)過![]() 點(diǎn)作
點(diǎn)作![]() 軸的垂線
軸的垂線![]() ,平行于
,平行于![]() 軸的兩條直線
軸的兩條直線![]() ,
, ![]() 分別交曲線
分別交曲線![]() 于
于![]() ,
, ![]() 兩點(diǎn)(直線
兩點(diǎn)(直線![]() 不過
不過![]() ),交
),交![]() 于
于![]() ,
, ![]() 兩點(diǎn).若線段
兩點(diǎn).若線段![]() 中點(diǎn)的軌跡方程為
中點(diǎn)的軌跡方程為![]() ,求
,求![]() 與
與![]() 的面積之比.
的面積之比.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com