
【題目】某班數學興趣小組對函數![]() 的圖象和性質將進行了探究,探究過程如下,請補充完整.
的圖象和性質將進行了探究,探究過程如下,請補充完整.
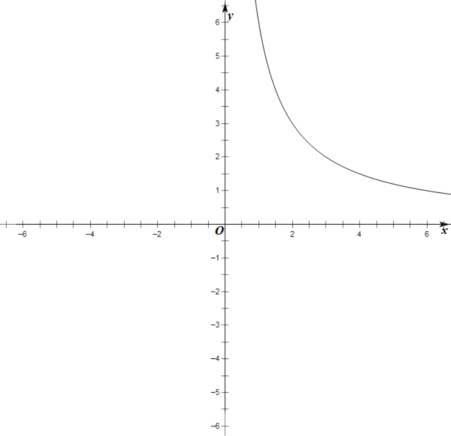
(1)自變量![]() 的取值范圍是除
的取值范圍是除![]() 外的全體實數,
外的全體實數,![]() 與
與![]() 的幾組對應值列表如下:
的幾組對應值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根據上表數據,在如圖所示的平面直角坐標系中描點并畫出了函數圖象的一部分,請畫出該函數圖象的另一部分;
(3)觀察函數圖象,寫出一條函數性質;
(4)進一步探究函數圖象發現:
①函數圖象與![]() 軸交點情況是________,所以對應方程
軸交點情況是________,所以對應方程![]() 的實數根的情況是________;
的實數根的情況是________;
②方程![]() 有_______個實數根;
有_______個實數根;
③關于![]() 的方程
的方程![]() 有
有![]() 個實數根,
個實數根,![]() 的取值范圍是________.
的取值范圍是________.
【答案】(1)![]() ;(2)圖象見解析;(3)函數
;(2)圖象見解析;(3)函數![]() 的單調遞減區間為
的單調遞減區間為![]() (答案不唯一);(4)①無交點,無實數根;②
(答案不唯一);(4)①無交點,無實數根;②![]() ;③
;③![]() .
.
【解析】
(1)把![]() 代入
代入![]() 求得
求得![]() 的值,即可得出
的值,即可得出![]() 的值;
的值;
(2)根據表格提供的數據描點,連線即可得到函數![]() 的另一部分圖象;
的另一部分圖象;
(3)觀察圖象,總結出函數的性質即可;
(4)①由于![]() 的值不能為
的值不能為![]() ,故函數值也不能為
,故函數值也不能為![]() ,從而可得出函數圖象與
,從而可得出函數圖象與![]() 軸無交點,因而
軸無交點,因而![]() 無實數根;
無實數根;
②方程![]() 的實數根的個數可以看作函數
的實數根的個數可以看作函數![]() 與直線
與直線![]() 的交點個數,畫出圖象即可得到結論;
的交點個數,畫出圖象即可得到結論;
③由②的圖象即可得到結果.
(1)把![]() 代入
代入![]() 得,
得,![]() ,所以,
,所以,![]() ;
;
(2)如圖所示:
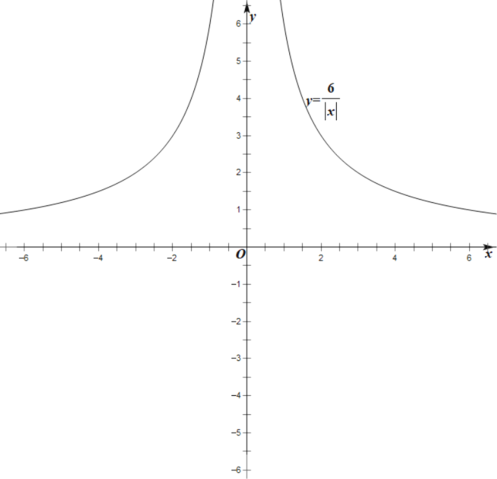
(3)觀察圖象可知,函數![]() 的單調遞減區間為
的單調遞減區間為![]() (答案不唯一);
(答案不唯一);
(4)①![]() ,
,![]() ,所以,函數
,所以,函數![]() 的圖象與
的圖象與![]() 軸無交點,則方程
軸無交點,則方程![]() 無實數根;
無實數根;
②求方程![]() 的根的個數,可以看成函數
的根的個數,可以看成函數![]() 與直線
與直線![]() 的交點個數,如圖,
的交點個數,如圖,
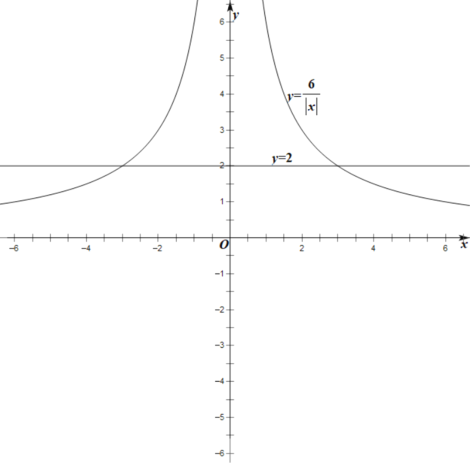
函數![]() 與直線
與直線![]() 有兩個交點,故方程
有兩個交點,故方程![]() 有
有![]() 個實數根,
個實數根,
③由②的圖象可以得出,關于![]() 的方程
的方程![]() 有
有![]() 個實數根,
個實數根,![]() 的取值范圍是
的取值范圍是![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為平行四邊形,PA⊥底面ABCD,
中,底面ABCD為平行四邊形,PA⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面PCA⊥平面PCD;
(2)設E為側棱PC上的一點,若直線BE與底面ABCD所成的角為45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】曲線![]() ,直線
,直線![]() 關于直線
關于直線![]() 對稱的直線為
對稱的直線為![]() ,直線
,直線![]() ,
,![]() 與曲線
與曲線![]() 分別交于點
分別交于點![]() 、
、![]() 和
和![]() 、
、![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() .
.
(Ⅰ)求證:![]() ;
;
(Ⅱ)當![]() 變化時,試問直線
變化時,試問直線![]() 是否恒過定點?若恒過定點,求出該定點坐標;若不恒過定點,請說明理由.
是否恒過定點?若恒過定點,求出該定點坐標;若不恒過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的非負半軸為極軸建立極坐標系,圓
軸的非負半軸為極軸建立極坐標系,圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點.
兩點.
(1)求圓![]() 的直角坐標方程及弦
的直角坐標方程及弦![]() 的長;
的長;
(2)動點![]() 在圓
在圓![]() 上(不與
上(不與![]() ,
, ![]() 重合),試求
重合),試求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】探究函數![]() 的圖象與性質.
的圖象與性質.
(1)下表是y與x的幾組對應值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值為_______________;
(2)根據上表數據,在如圖所示的平面直角坐標系中描點,并已畫出了函數圖象的一部分,請你畫出該圖象的另一部分;

(3)結合函數的圖象,寫出該函數的一條性質:_________;
(4)若關于x的方程![]() 有2個實數根,則t的取值范圍是______.
有2個實數根,則t的取值范圍是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個函數當自變量在不同范圍內取值時,函數表達式不同,我們稱這樣的函數為分段函數.下面我們參照學習函數的過程與方法,探究分段函數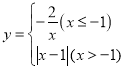 的圖象與性質.列表:
的圖象與性質.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描點:在平面直角坐標系中,以自變量x的取值為橫坐標,以相應的函數值y為縱坐標,描出相應的點,如圖所示.
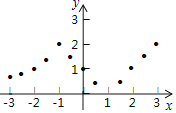
(1)如圖,在平面直角坐標系中,觀察描出的這些點的分布,作出函數圖象;
(2)研究函數并結合圖象與表格,回答下列問題:
①點![]() ,
,![]() ,
,![]() ,
,![]() 在函數圖象上,
在函數圖象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②當函數值![]() 時,求自變量x的值;
時,求自變量x的值;
③在直線![]() 的右側的函數圖象上有兩個不同的點
的右側的函數圖象上有兩個不同的點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直線![]() 與函數圖象有三個不同的交點,求a的取值范圍.
與函數圖象有三個不同的交點,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地有南北街道5條,東西街道5條,現在甲、乙、丙3名郵遞員從該地西南角的郵局![]() 出發,送信到東北角的
出發,送信到東北角的![]() 地,要求所走路程最短,設圖中點
地,要求所走路程最短,設圖中點![]() ,
,![]() ,
,![]() 是交叉路口,且
是交叉路口,且![]() 路段由于修路不能通行.
路段由于修路不能通行.
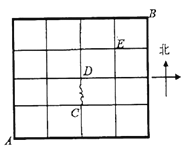
(1)求甲從![]() 到
到![]() 共有多少種走法?(用數字作答)
共有多少種走法?(用數字作答)
(2)求甲經過點![]() 的概率;
的概率;
(3)設3名郵遞員恰有![]() 名郵遞員經過點
名郵遞員經過點![]() ,求隨機變量
,求隨機變量![]() 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,第1個圖形由正三角形擴展而成,共12個頂點.第n個圖形是由正n+2邊形擴展而來 ![]() ,則第n+1個圖形的頂點個數是 ( )
,則第n+1個圖形的頂點個數是 ( )
 (1)
(1)  (2)
(2) (3)
(3)  (4)
(4)
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某服裝批發市場1-5月份的服裝銷售量![]() 與利潤
與利潤![]() 的統計數據如下表:
的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷售量 | 3 | 6 | 4 | 7 | 8 |
利潤 | 19 | 34 | 26 | 41 | 46 |
(1)從這五個月的利潤中任選2個,分別記為![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知銷售量![]() 與利潤
與利潤![]() 大致滿足線性相關關系,請根據前4個月的數據,求出
大致滿足線性相關關系,請根據前4個月的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的利潤的估計數據與真實數據的誤差不超過2萬元,則認為得到的利潤的估計數據是理想的.請用表格中第5個月的數據檢驗由(2)中回歸方程所得的第5個月的利潤的估計數據是否理想.參考公式:  .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com