
【題目】已知拋物線![]() :
:![]() ,
,![]() ,
,![]() 是拋物線
是拋物線![]() 上的兩點,
上的兩點,![]() 是坐標原點,且
是坐標原點,且![]() .
.
(1)若![]() ,求
,求![]() 的面積;
的面積;
(2)設(shè)![]() 是線段
是線段![]() 上一點,若
上一點,若![]() 與
與![]() 的面積相等,求
的面積相等,求![]() 的軌跡方程.
的軌跡方程.
【答案】(1)16(2) ![]()
【解析】
分析:(1)![]() ,由拋物線的對稱性可知
,由拋物線的對稱性可知![]() ,
,![]() 關(guān)于
關(guān)于![]() 軸對稱設(shè)出點的關(guān)系;
軸對稱設(shè)出點的關(guān)系;![]() ,求出
,求出![]() ,
,![]() 點的坐標,求出面積。
點的坐標,求出面積。
![]() 與
與![]() 的面積相等,所以
的面積相等,所以![]() 為
為![]() 的中點,利用消參法求出軌跡方程
的中點,利用消參法求出軌跡方程
詳解:設(shè)![]() ,
,![]() ,
,
(1)因為![]() ,
,
又由拋物線的對稱性可知![]() ,
,![]() 關(guān)于
關(guān)于![]() 軸對稱,
軸對稱,
所以![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,故
,故![]() ,
,
則![]() ,又
,又![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() ,于是
,于是![]() 的面積為
的面積為![]() .
.
(2)直線![]() 的斜率存在,設(shè)直線
的斜率存在,設(shè)直線![]() 的方程為
的方程為![]() ,
,
代入![]() ,得
,得![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ,
,
故![]() ,則
,則![]() ,
,
所以![]() 或
或![]() (舍),
(舍),
因為![]() 與
與![]() 的面積相等,所以
的面積相等,所以![]() 為
為![]() 的中點,
的中點,
則![]() 點的橫坐標為
點的橫坐標為![]() ,縱坐標為
,縱坐標為![]() ,
,
故![]() 點的軌跡方程為
點的軌跡方程為![]() .
.
點晴:圓錐曲線類的題目,畫出相應(yīng)的草圖,對題目給出的關(guān)鍵信息進行分析轉(zhuǎn)化是做題的要點,然后選取相應(yīng)的方法進行解決問題,計算量較大,計算的過程中含參的較多,大家要做到多想少算。


 優(yōu)等生題庫系列答案
優(yōu)等生題庫系列答案科目:高中數(shù)學 來源: 題型:
【題目】某學校為了分析在一次數(shù)學競賽中甲、乙兩個班的數(shù)學成績,分別從甲、乙兩個班中隨機抽取了10個學生的成績,成績的莖葉圖如下:
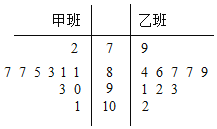
(Ⅰ)根據(jù)莖葉圖,計算甲班被抽取學生成績的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若規(guī)定成績不低于90分的等級為優(yōu)秀,現(xiàn)從甲、乙兩個班級所抽取成績等級為優(yōu)秀的學生中,隨機抽取2人,求這兩個人恰好都來自甲班的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知一定點![]() ,及一定直線
,及一定直線![]() :
:![]() ,以動點
,以動點![]() 為圓心的圓
為圓心的圓![]() 過點
過點![]() ,且與直線
,且與直線![]() 相切.
相切.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設(shè)![]() 在直線
在直線![]() 上,直線
上,直線![]() ,
,![]() 分別與曲線
分別與曲線![]() 相切于
相切于![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點.求證:
的中點.求證:![]() ,且直線
,且直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平均值為2,方差為1,則數(shù)據(jù)
的平均值為2,方差為1,則數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() 相對于原數(shù)據(jù)( )
相對于原數(shù)據(jù)( )
A.一樣穩(wěn)定B.變得比較穩(wěn)定C.變得比較不穩(wěn)定D.穩(wěn)定性不可以判斷
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知向量![]() ,
,![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() .
.
(1)若函數(shù)![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱,且
對稱,且![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)在(1)的條件下,當![]() 時,函數(shù)
時,函數(shù)![]() 有且只有一個零點,求實數(shù)
有且只有一個零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ;
;
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)實數(shù)![]() 為
為![]() 的最大值,若實數(shù)
的最大值,若實數(shù)![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ;
;
(1)求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)實數(shù)![]() 為
為![]() 的最大值,若實數(shù)
的最大值,若實數(shù)![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com