
【題目】為了美化環境,某公園欲將一塊空地規劃建成休閑草坪,休閑草坪的形狀為如圖所示的四邊形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=
百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).

(1)當cos![]() =
=![]() 時,求小路AC的長度;
時,求小路AC的長度;
(2)當草坪ABCD的面積最大時,求此時小路BD的長度.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)在△ABD中,由余弦定理可求BD的值,利用同角三角函數基本關系式可求sinθ,根據正弦定理可求sin∠ADB![]() ,進而可求cos∠ADC的值,在△ACD中,利用余弦定理可求AC的值.
,進而可求cos∠ADC的值,在△ACD中,利用余弦定理可求AC的值.
(2)由(1)得:BD2=14﹣6![]() cosθ,根據三角形面積公式,三角函數恒等變換的應用可求.SABCD=7
cosθ,根據三角形面積公式,三角函數恒等變換的應用可求.SABCD=7![]() sin(θ﹣φ),結合題意當θ﹣φ
sin(θ﹣φ),結合題意當θ﹣φ![]() 時,四邊形ABCD的面積最大,即θ=φ
時,四邊形ABCD的面積最大,即θ=φ![]() ,此時cosφ
,此時cosφ![]() ,sinφ
,sinφ![]() ,從而可求BD的值.
,從而可求BD的值.
(1)在![]() 中,由
中,由![]() ,
,
得![]() ,又
,又![]() ,∴
,∴![]() .
.
∵![]() ∴
∴![]()
由![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∵![]() 是以
是以![]() 為直角頂點的等腰直角三角形 ∴
為直角頂點的等腰直角三角形 ∴![]() 且
且![]()
∴![]()
在![]() 中,
中,![]()
![]() ,
,
解得:![]()
(2)由(1)得:![]() ,
,
![]()
![]()
![]() ,此時
,此時![]() ,
,![]() ,且
,且![]()
當![]() 時,四邊形
時,四邊形![]() 的面積最大,即
的面積最大,即![]() ,此時
,此時![]() ,
,![]()
∴![]() ,即
,即![]()
答:當![]() 時,小路
時,小路![]() 的長度為
的長度為![]() 百米;草坪
百米;草坪![]() 的面積最大時,小路
的面積最大時,小路![]() 的長度為
的長度為![]() 百米.
百米.


 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】田忌賽馬是![]() 史記
史記![]() 中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等
中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等![]() 于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注
于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注![]() 假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
田忌的馬 | 上等馬 | 中等馬 | 下等馬 |
上等馬 |
|
| 1 |
中等馬 |
|
|
|
下等馬 | 0 |
|
|
比賽規則規定:一次比由三場賽馬組成,每場由公子和田忌各出一匹馬出騫,結果只有勝和負兩種,并且毎一方三場賽馬的馬的等級各不相同,三場比賽中至少獲勝兩場的一方為最終勝利者.
![]() 如果按孫臏的策略比賽一次,求田忌獲勝的概率;
如果按孫臏的策略比賽一次,求田忌獲勝的概率;
![]() 如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場的空調在1月到5月的銷售量與月份相關,得到的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)經分析發現1月到5月的銷售量可用線性回歸模型擬合該商場空調的月銷量![]() (百件)與月份
(百件)與月份![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測6月份該商場空調的銷售量;
,并預測6月份該商場空調的銷售量;
(2)若該商場的營銷部對空調進行新一輪促銷,對7月到12月有購買空調意愿的顧客進行問卷調查.假設該地擬購買空調的消費群體十分龐大,經過營銷部調研機構對其中的500名顧客進行了一個抽樣調查,得到如下一份頻數表:
有購買意愿對應的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
頻數 | 60 | 80 | 120 | 130 | 80 | 30 |
現采用分層抽樣的方法從購買意愿的月份在7月與12月的這90名顧客中隨機抽取6名,再從這6人中隨機抽取3人進行跟蹤調查,求抽出的3人中恰好有2人是購買意愿的月份是12月的概率.
參考公式與數據:線性回歸方程![]() ,其中
,其中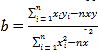 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩人各有三張卡片,甲的卡片分別標有數字1、2、3,乙的卡片分別標有數字0、1、3.兩人各自隨機抽出一張,甲抽出的卡片上的數字記為![]() ,乙抽出的卡片上的數字記為
,乙抽出的卡片上的數字記為![]() ,則
,則![]() 與
與![]() 的積為奇數的概率為________.
的積為奇數的概率為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然對數的底數,e≈2.718…).
(1)求函數f(x)的極值;
(2)若函數y=f(x)g(x)在區間[1,2]上單調遞增,求實數a的取值范圍;
(3)若函數h(x)=![]() 在區間(0,+∞)上既存在極大值又存在極小值,并且函數h(x)的極大值小于整數b,求b的最小值.
在區間(0,+∞)上既存在極大值又存在極小值,并且函數h(x)的極大值小于整數b,求b的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
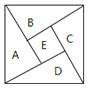
【題目】如圖為我國數學家趙爽![]() 約3世紀初
約3世紀初![]() 在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不同,則
在為《周髀算經》作注時驗證勾股定理的示意圖,現在提供5種顏色給其中5個小區域涂色,規定每個區域只涂一種顏色,相鄰區域顏色不同,則![]() 區域涂色不相同的概率為
區域涂色不相同的概率為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中點(如圖1),將
是EA的中點(如圖1),將![]() 沿CD折起到圖2中
沿CD折起到圖2中![]() 的位置,得到四棱錐是
的位置,得到四棱錐是![]() .
.
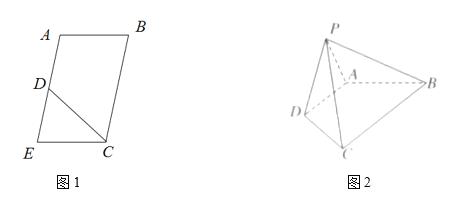
(1)求證:![]() 平面PDA;
平面PDA;
(2)若PD與平面ABCD所成的角為![]() .且
.且![]() 為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
為銳角三角形,求平面PAD和平面PBC所成銳二面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com