Question

【題目】在平面直角坐標系中，以坐標原點為極點，軸的正半軸為極軸建立極坐標系，已知曲線的極坐標方程為，過點的直線的參數(shù)方程為（為參數(shù)），直線與曲線相交于，兩點.

（1）寫出曲線的直角坐標方程和直線的普通方程；

（2）若，求的值.

Answer 1

【答案】（1）曲線的直角坐標方程，直線的普通方程為；（2）。

【解析】

（1）利用代入法消去直線的參數(shù)方程中的參數(shù)，可得其普通方程，曲線的極坐標方程兩邊同乘以，利用 即可得到曲線的直角坐標方程；（2）直線的參數(shù)方程代入曲線的直角坐標方程，利用韋達定理、直線參數(shù)方程的幾何意義可得結(jié)果.

（1）由得，

所以曲線的直角坐標方程，

因為，所以，

直線的普通方程為；

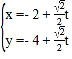（2）直線的參數(shù)方程為（為參數(shù)），

代入得：，

設，對應的參數(shù)分別為，，

則，，，

由參數(shù)，的幾何意義得，，，

由得，所以，

所以，即，

故，或（舍去），

所以.