如圖,在正三棱錐
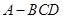
中,
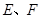
分別是
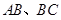
的中點,
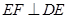
,且
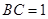
,則正三棱錐
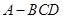
的體積是( )
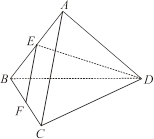
試題分析:如圖,取線段
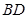
的中點
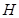
,連接
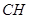
,則依題意可知
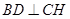
,且頂點
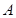
在底面

的射影
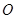
落在
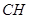
上,所以由
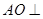
面

可得
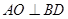
,而
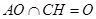
,所以由線面垂直的判定定理可得
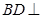
平面
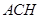
,所以有
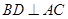
,而
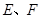
是邊
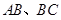
的中點,所以

,而
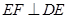
,所以
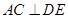
,而
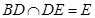
,由線面垂直的判定定理又可以得到
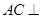
平面
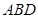
,再結(jié)合三棱錐
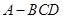
為正三棱錐且
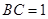
,所以該正三棱錐的側(cè)棱兩兩垂直且
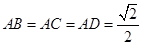
,所以
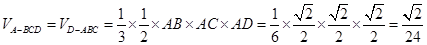
,故選B.

練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,四邊形
ABCD是邊長為2的正方形,直線
l與平面
ABCD平行,
E和
F是
l上的兩個不同點,且
EA=
ED,
FB=
FC.
E′和
F′是平面
ABCD內(nèi)的兩點,
EE′和
FF′都與平面
ABCD垂直.
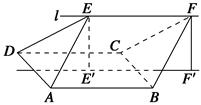
(1)證明:直線
E′
F′垂直且平分線段
AD;
(2)若∠
EAD=∠
EAB=60 °,
EF=2.求多面體
ABCDEF的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在四棱錐

中,底面

為直角梯形,且
,

,平面

底面

,

為

的中點,

是棱

的中點,

.
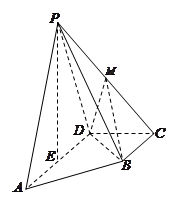

(Ⅰ)求證:

平面

;
(Ⅱ)求三棱錐

的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,三棱柱ABC-A
1B
1C
1的側(cè)棱AA
1⊥平面ABC,△ABC為正三角形,且側(cè)面AA
1C
1C是邊長為2的正方形,E是
的中點,F在棱CC
1上。
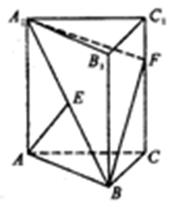
(1)當(dāng)
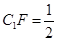
CF時,求多面體ABCFA
1的體積;
(2)當(dāng)點F使得A
1F+BF最小時,判斷直線AE與A
1F是否垂直,并證明的結(jié)論。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
側(cè)面都是直角三角形的正三棱錐,底面邊長為a時,該三棱錐的全面積是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知矩形
ABCD的頂點都在半徑為5的球
O的球面上,且
AB=8,
BC=2
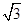
,則棱錐
O-ABCD的體積為________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
棱長為1的正方體的八個頂點都在同一個球面上,則此球的表面積為 .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
一個底面為正三角形,側(cè)棱與底面垂直的棱柱,其三視圖如圖所示,則這個棱柱的體積為
______.
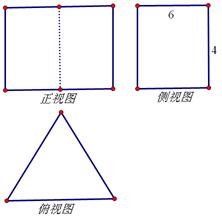
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在四棱錐
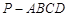
中,底面

是邊長為
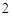
的菱形,
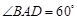
,側(cè)棱
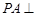
底面

,
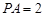
,
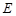
為
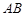
的中點,則四面體

的體積為
.
查看答案和解析>>

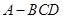 中,
中,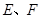 分別是
分別是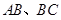 的中點,
的中點,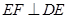 ,且
,且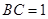 ,則正三棱錐
,則正三棱錐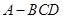 的體積是( )
的體積是( )
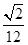
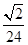
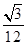
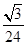

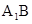 的中點,F在棱CC1上。
的中點,F在棱CC1上。
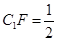 CF時,求多面體ABCFA1的體積;
CF時,求多面體ABCFA1的體積;