解:(1)顯然f(x)在區間上為增函數(0,1],
因為

=
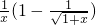
=
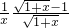
=
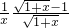
=
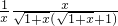
=
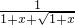
,
所以

在區間(0,1]上為減函數.
所以f(x)在區間(0,1]上為“弱減函數”.
(2)證法1:要證|f(x
2)-f(x
1)|<
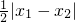
,不妨設0≤x
1<x
2,
由f(x)=1-

在[0,+∞)單調遞增,
得f(x
2)>f(x
1),
那么只要證f(x
2)-f(x
1)<
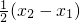
,
即證f(x
2)-
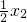
<f(x
1)-

.
令g(x)=f(x)-

,則問題轉化為只要證明g(x)=f(x)-

在[0,+∞)單調遞減即可.
事實上,g(x)=f(x)-

=1-

-

,
當x∈[0,+∞)時,g′(x)=
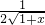
-

≤0,
所以g(x)=f(x)-

在[0,+∞)單調遞減,
故命題成立.
證法2:|f(x
2)-f(x
1)|=

=
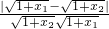
=
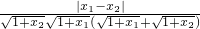
,
因為x
1,x
2∈[0,+∞),且x
1≠x
2,
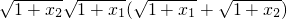
>2,
所以|f(x
2)-f(x
1)|<
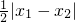
.
(3)當x∈[0,1]時,不等式1-ax≤

≤1-bx恒成立.
當x=0時,不等式顯然成立.
當x∈(0,1]時,等價于
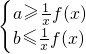
恒成立.
由(1)知

為減函數,1-

≤

<

,
所以a≥

且b≤1-

.
分析:(1)根據弱增函數的定義,只需證明函數f(x)在區間(0,1]上是增函數,而函數

為減函數,即可;
(2)證法1:要證|f(x
2)-f(x
1)|<
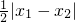
,不妨設0≤x
1<x
2,構造函數g(x)=f(x)-

,利用導數證明該函數在(0,+∞)單調遞減即可證明結論;
證法2:把f(x)=1-

代入|f(x
2)-f(x
1)|,利用分母有理化,即可證明結論;
(3)要解)當x∈[0,1]時,不等式1-ax≤

≤1-bx恒成立,利用分離參數轉化為當x∈(0,1]時,等價于
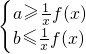
恒成立,即可求得實數a,b的取值范圍.
點評:此題是個難題.考查基本初等函數的單調性,以及構造函數證明不等式和恒成立問題,綜合性強,方法靈活,很好的考查了同學們觀察、推理以及創造性地分析問題、解決問題的能力.

 為減函數,則稱函數f(x)為“弱增函數”.已知函數f(x)=1-
為減函數,則稱函數f(x)為“弱增函數”.已知函數f(x)=1- .
.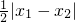 ;
; ≤1-bx恒成立,求實數a,b的取值范圍.
≤1-bx恒成立,求實數a,b的取值范圍. =
=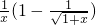 =
=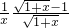 =
=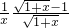 =
=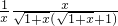 =
=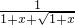 ,
, 在區間(0,1]上為減函數.
在區間(0,1]上為減函數.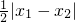 ,不妨設0≤x1<x2,
,不妨設0≤x1<x2, 在[0,+∞)單調遞增,
在[0,+∞)單調遞增,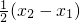 ,
,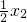 <f(x1)-
<f(x1)- .
. ,則問題轉化為只要證明g(x)=f(x)-
,則問題轉化為只要證明g(x)=f(x)- 在[0,+∞)單調遞減即可.
在[0,+∞)單調遞減即可. =1-
=1- -
- ,
,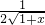 -
- ≤0,
≤0, 在[0,+∞)單調遞減,
在[0,+∞)單調遞減, =
=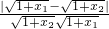
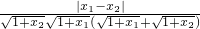 ,
,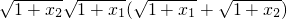 >2,
>2,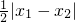 .
. ≤1-bx恒成立.
≤1-bx恒成立.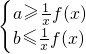 恒成立.
恒成立. 為減函數,1-
為減函數,1- ≤
≤ <
< ,
, 且b≤1-
且b≤1- .
. 為減函數,即可;
為減函數,即可;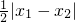 ,不妨設0≤x1<x2,構造函數g(x)=f(x)-
,不妨設0≤x1<x2,構造函數g(x)=f(x)- ,利用導數證明該函數在(0,+∞)單調遞減即可證明結論;
,利用導數證明該函數在(0,+∞)單調遞減即可證明結論; 代入|f(x2)-f(x1)|,利用分母有理化,即可證明結論;
代入|f(x2)-f(x1)|,利用分母有理化,即可證明結論; ≤1-bx恒成立,利用分離參數轉化為當x∈(0,1]時,等價于
≤1-bx恒成立,利用分離參數轉化為當x∈(0,1]時,等價于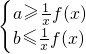 恒成立,即可求得實數a,b的取值范圍.
恒成立,即可求得實數a,b的取值范圍.

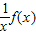 為減函數,則稱函數f(x)為“弱增”函數.已知函數
為減函數,則稱函數f(x)為“弱增”函數.已知函數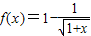 .
.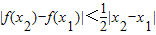 ;
;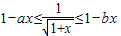 恒成立,求實數a,b的取值范圍.
恒成立,求實數a,b的取值范圍. 為減函數,則稱函數f(x)為“弱增函數”.已知函數f(x)=1-
為減函數,則稱函數f(x)為“弱增函數”.已知函數f(x)=1-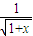 .
. ;
; ≤1-bx恒成立,求實數a,b的取值范圍.
≤1-bx恒成立,求實數a,b的取值范圍.