
【題目】已知函數(shù)f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函數(shù)f(x)的定義域;
(2)討論函數(shù)f(x)的奇偶性;
(3)求a的取值范圍,使f(x)>0在定義域上恒成立.
【答案】(1){x|x∈R,且x≠0}(2)偶函數(shù)(3)a>1.
【解析】
(1)由于ax-1≠0,則ax≠1,所以x≠0,
所以函數(shù)f(x)的定義域為{x|x∈R,且x≠0}.
(2)對于定義域內(nèi)任意的x,有
f(-x)=![]() (-x)3=-
(-x)3=-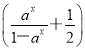 x3=-
x3=-![]() x3=
x3=![]() x3=f(x)所以f(x)是偶函數(shù).
x3=f(x)所以f(x)是偶函數(shù).
(3)①當(dāng)a>1時,對x>0,
所以ax>1,即ax-1>0,所以![]() +
+![]() >0.
>0.
又x>0時,x3>0,所以x3![]() >0,
>0,
即當(dāng)x>0時,f(x)>0.
由(2)知,f(x)是偶函數(shù),即f(-x)=f(x),
則當(dāng)x<0時,-x>0,有f(-x)=f(x)>0成立.
綜上可知,當(dāng)a>1時,f(x)>0在定義域上恒成立.
②當(dāng)0<a<1時,f(x)=![]() ,
,
當(dāng)x>0時,0<ax<1,此時f(x)<0,不滿足題意;
當(dāng)x<0時,-x>0,有f(-x)=f(x)<0,也不滿足題意.
綜上可知,所求a的取值范圍是a>1


 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】通過市場調(diào)查,得到某種產(chǎn)品的資金投入x(單位:萬元)與獲得的利潤y(單位:萬元)的數(shù)據(jù),如表所示:
資金投入x | 2 | 3 | 4 | 5 | 6 |
利潤y | 2 | 3 | 5 | 6 | 9 |
(1)畫出數(shù)據(jù)對應(yīng)的散點圖;
(2)根據(jù)上表提供的數(shù)據(jù),用最小二乘法求線性回歸直線方程![]() ;
;
(3)現(xiàn)投入資金10萬元,求獲得利潤的估計值為多少萬元?
參考公式:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】恩施州某電影院共有1000個座位,票價不分等次,根據(jù)電影院的經(jīng)營經(jīng)驗,當(dāng)每張票價不超過10元時、票可全部售出;當(dāng)票價高于10元時,每提高1元,將有30張票不能售出,為了獲得更好的收入,需要給電影院一個合適的票價,基本條件是:①為了方便找零和算賬,票價定為1元的整數(shù)倍.②影院放映一場電影的成本是4000元,票房收入必須高于成本,用x(元)表示每張票價,用y(元)表示該電影放映一場的純收入(除去成本后的收入).
(1)求函數(shù)y=f(x)的解析式;
(2)票價定為多少時,電影放映一場的純收入最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次人才招聘會上,有![]() 、
、![]() 兩家公司分別開出了他們的工資標(biāo)準(zhǔn):
兩家公司分別開出了他們的工資標(biāo)準(zhǔn):![]() 公司允諾第一個月工資為8000元,以后每年月工資比上一年月工資增加500元;
公司允諾第一個月工資為8000元,以后每年月工資比上一年月工資增加500元;![]() 公司允諾第一年月工資也為8000元,以后每年月工資在上一年的月工資基礎(chǔ)上遞增
公司允諾第一年月工資也為8000元,以后每年月工資在上一年的月工資基礎(chǔ)上遞增![]() ,設(shè)某人年初被
,設(shè)某人年初被![]() 、
、![]() 兩家公司同時錄取,試問:
兩家公司同時錄取,試問:
(1)若該人分別在![]() 公司或
公司或![]() 公司連續(xù)工作
公司連續(xù)工作![]() 年,則他在第
年,則他在第![]() 年的月工資分別是多少;
年的月工資分別是多少;
(2)該人打算連續(xù)在一家公司工作10年,僅從工資收入總量較多作為應(yīng)聘的標(biāo)準(zhǔn)(不計其他因素),該人應(yīng)該選擇哪家公司,為什么?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 平面上有一點列
平面上有一點列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,對每個正整數(shù)
,對每個正整數(shù)![]() ,點
,點![]() 位于函數(shù)
位于函數(shù)![]()
![]() 的圖像上,且點
的圖像上,且點![]() 、點
、點![]() 與點
與點![]() 構(gòu)成一個以
構(gòu)成一個以![]() 為頂角頂點的等腰三角形;
為頂角頂點的等腰三角形;
(1)求點![]() 的縱坐標(biāo)
的縱坐標(biāo)![]() 的表達(dá)式;
的表達(dá)式;
(2)若對每個自然數(shù)![]() ,以
,以![]() 、
、![]() 、
、![]() 為邊長能構(gòu)成一個三角形,求
為邊長能構(gòu)成一個三角形,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]()
![]() ,若
,若![]() 取(2)中確定的范圍內(nèi)的最小整數(shù),問數(shù)列
取(2)中確定的范圍內(nèi)的最小整數(shù),問數(shù)列![]() 的最大項的項數(shù)是多少?試說明理由;
的最大項的項數(shù)是多少?試說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】雙曲線![]()
![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過
,過![]() 作傾斜角為
作傾斜角為![]() 的直線與
的直線與![]() 軸和雙曲線的右支分別交于
軸和雙曲線的右支分別交于![]() 兩點,若點
兩點,若點![]() 平分線段
平分線段![]() ,則該雙曲線的離心率是( )
,則該雙曲線的離心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,設(shè)橢圓中心在原點,焦點在![]() 軸上,
軸上,![]()
![]() 為橢圓長軸的兩個端點,
為橢圓長軸的兩個端點,![]() 為橢圓的右焦點.已知橢圓的離心率為
為橢圓的右焦點.已知橢圓的離心率為![]() ,且
,且![]() .
.

(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 是橢圓上位于
是橢圓上位于![]() 軸上方的一個動點,直線
軸上方的一個動點,直線![]() ,
,![]() 分別與直線
分別與直線![]() 相交于點
相交于點![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 經(jīng)過原點
經(jīng)過原點![]() 且與直線
且與直線![]() 相切于點
相切于點![]()
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)在圓![]() 上是否存在兩點
上是否存在兩點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,且以線段
對稱,且以線段![]() 為直徑的圓經(jīng)過原點?若存在,寫出直線
為直徑的圓經(jīng)過原點?若存在,寫出直線![]() 的方程;若不存在,請說明理由
的方程;若不存在,請說明理由
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)a=3時,方程![]() 的解的個數(shù);
的解的個數(shù);
(2)對任意![]() 時,函數(shù)
時,函數(shù)![]() 的圖象恒在函數(shù)
的圖象恒在函數(shù)![]() 圖象的下方,求a的取值范圍;
圖象的下方,求a的取值范圍;
(3)![]() 在
在![]() 上單調(diào)遞增,求a的范圍;
上單調(diào)遞增,求a的范圍;
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com