
【題目】正方體![]() 中,
中,![]() 為
為![]() 中點(diǎn),
中點(diǎn),![]() 為
為![]() 中點(diǎn),則異面直線
中點(diǎn),則異面直線![]() 與
與![]() 所成角的余弦值為____.
所成角的余弦值為____.
【答案】![]()
【解析】
解法一:連結(jié)![]() ,可證得
,可證得![]() 為異面直線
為異面直線![]() 與
與![]() 所成角或其補(bǔ)角,然后在
所成角或其補(bǔ)角,然后在![]() 中利用余弦定理可求得結(jié)果;
中利用余弦定理可求得結(jié)果;
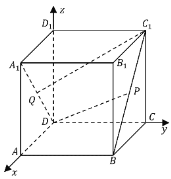
解法二:如圖,以![]() 為原點(diǎn),分別以
為原點(diǎn),分別以![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸的正方向,建立空間直角坐標(biāo)系
軸的正方向,建立空間直角坐標(biāo)系![]() ,利用向量法求解;
,利用向量法求解;
解法三:由于,所以以![]() 為基底,將
為基底,將![]() ,
,![]() 用基底表示出來,再向量夾角公式求解.
用基底表示出來,再向量夾角公式求解.
解法一:連結(jié)![]() ,因?yàn)樗倪呅?/span>
,因?yàn)樗倪呅?/span>![]() 為正方形,
為正方形,![]() 為
為![]() 中點(diǎn),所以
中點(diǎn),所以![]() .因?yàn)?/span>
.因?yàn)?/span>![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,又
,又![]() 為
為![]() 中點(diǎn),所以
中點(diǎn),所以![]() ,所以四邊形
,所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,
,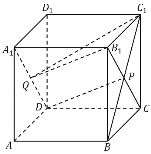
所以![]() 為異面直線
為異面直線![]() 與
與![]() 所成角或其補(bǔ)角.設(shè)正方體的棱長為2,在
所成角或其補(bǔ)角.設(shè)正方體的棱長為2,在![]() 中,
中,![]() ;
;
同理可求![]() .在
.在![]() 中,
中,
![]() ,
,
故異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
解法二:如圖,以![]() 為原點(diǎn),分別以
為原點(diǎn),分別以![]() 的方向?yàn)?/span>
的方向?yàn)?/span>![]() 軸的正方向,建立空間直角坐標(biāo)系
軸的正方向,建立空間直角坐標(biāo)系![]() .設(shè)正方體的棱長為2,則各點(diǎn)的坐標(biāo)為
.設(shè)正方體的棱長為2,則各點(diǎn)的坐標(biāo)為![]()
![]()
![]() ,所以
,所以![]() ,
,
所以![]()
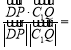
![]()
![]() .
.
所以異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
解法三:設(shè)正方體的棱長為2,![]()
則![]() ,
,![]() ,
,
由![]() 三條直線兩兩垂直得
三條直線兩兩垂直得![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]()
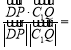
![]()
![]() .
.
所以異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
故答案為:![]()


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
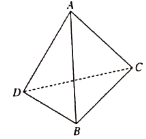
【題目】現(xiàn)有一副斜邊長為10的直角三角板,將它們斜邊![]() 重合,若將其中一個(gè)三角板沿斜邊折起形成三棱錐
重合,若將其中一個(gè)三角板沿斜邊折起形成三棱錐![]() ,如圖所示,已知
,如圖所示,已知![]() ,
,![]() ,則三棱錐
,則三棱錐![]() 的外接球的表面積為______;該三棱錐體積的最大值為_______.
的外接球的表面積為______;該三棱錐體積的最大值為_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的圖象如圖所示,給出四個(gè)函數(shù):①
的圖象如圖所示,給出四個(gè)函數(shù):①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,又給出四個(gè)函數(shù)的圖象,則正確的匹配方案是( ).
,又給出四個(gè)函數(shù)的圖象,則正確的匹配方案是( ).
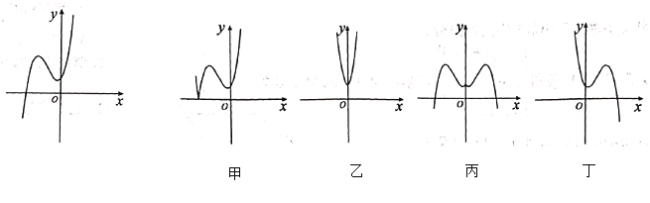
A.①-甲,②-乙,③-丙,④-丁B.②-甲,①-乙,③-丙,④-丙
C.①-甲,③-乙,④-丙,②-丁D.①-甲,④-乙,③-丙,②-丁
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】采購經(jīng)理指數(shù)(PMⅠ)是衡量一個(gè)國家制造業(yè)的“體檢表”,是衡量制造業(yè)在生產(chǎn)、新訂單、商品價(jià)格、存貨、雇員、訂單交貨新出口訂單和進(jìn)口等八個(gè)方面狀況的指數(shù),圖為2018年9月—2019年9月我國制造業(yè)的采購經(jīng)理指數(shù)(單位:%).
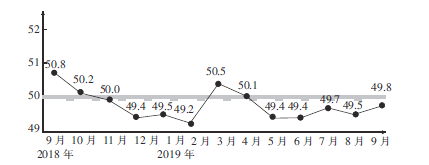
(1)求2019年前9個(gè)月我國制造業(yè)的采購經(jīng)理指數(shù)的平均數(shù)(精確到0.1);
(2)從2018年10月—2019年9月這12個(gè)月任意選取4個(gè)月,記采購經(jīng)理指數(shù)與上個(gè)月相比有所回升的月份個(gè)數(shù)為X,求X的分布列與期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對(duì)![]() 四件參賽作品只評(píng)一件一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲,乙,丙,丁四位同學(xué)對(duì)這四件參賽作品預(yù)測如下:
四件參賽作品只評(píng)一件一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲,乙,丙,丁四位同學(xué)對(duì)這四件參賽作品預(yù)測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎(jiǎng)”; 乙說:“
作品獲得一等獎(jiǎng)”; 乙說:“ ![]() 作品獲得一等獎(jiǎng)”;
作品獲得一等獎(jiǎng)”;
丙說:“ ![]() 兩件作品未獲得一等獎(jiǎng)”; 丁說:“是
兩件作品未獲得一等獎(jiǎng)”; 丁說:“是![]() 作品獲得一等獎(jiǎng)”.
作品獲得一等獎(jiǎng)”.
評(píng)獎(jiǎng)揭曉后,發(fā)現(xiàn)這四位同學(xué)中只有兩位說的話是對(duì)的,則獲得一等獎(jiǎng)的作品是_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).設(shè)
為參數(shù)).設(shè)![]() 與
與![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,當(dāng)
,當(dāng)![]() 變化時(shí),
變化時(shí),![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)設(shè)![]() 為圓
為圓![]() 上任意一點(diǎn),求
上任意一點(diǎn),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以平面直角坐標(biāo)系的原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,將曲線
,將曲線![]() 繞極點(diǎn)逆時(shí)針旋轉(zhuǎn)
繞極點(diǎn)逆時(shí)針旋轉(zhuǎn)![]() 后得到曲線
后得到曲線![]() .
.
(Ⅰ)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(Ⅱ)若直線![]() :
:![]() 與
與![]() ,
,![]() 分別相交于異于極點(diǎn)的
分別相交于異于極點(diǎn)的![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】謝賓斯基三角形是一種分形,由波蘭數(shù)學(xué)家謝賓斯基在1915年提出,先作一個(gè)正三角形挖去一個(gè)“中心三角形”(即以原三角形各邊的中點(diǎn)為頂點(diǎn)的三角形),然后在剩下的小三角形中又挖去一個(gè)“中心三角形”,我們用白色代表挖去的面積,那么黑三角形為剩下的面積(我們稱黑三角形為謝賓斯基三角形).向圖中第4個(gè)大正三角形中隨機(jī)撒512粒大小均勻的細(xì)小顆粒物,則落在白色區(qū)域的細(xì)小顆粒物的數(shù)量約是( )
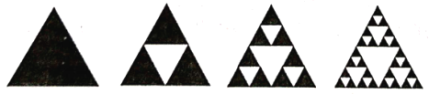
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)P為直線![]() 上任意一點(diǎn),
上任意一點(diǎn),![]() ,M為平面內(nèi)一點(diǎn),且
,M為平面內(nèi)一點(diǎn),且![]() .
.
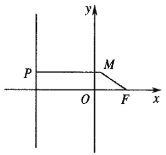
(Ⅰ)求點(diǎn)M的軌跡E的方程;
(Ⅱ)過點(diǎn)P作曲線E的切線,切點(diǎn)分別是![]() .若
.若![]() ,求點(diǎn)P的坐標(biāo).
,求點(diǎn)P的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com