
【題目】已知函數f(x)=x(1-![]() )是R上的偶函數.
)是R上的偶函數.
(1)對任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求實數m的取值范圍.
≥2x+1恒成立,求實數m的取值范圍.
(2)令g(x)=1-![]() ,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
【答案】(1)實數m的取值范圍為[3,+∞).(2)實數n的取值范圍是(2,+∞).
【解析】試題分析:(1)先根據偶函數得a=2,再分離變量得m≥2x-1最大值,即得實數m的取值范圍(2)根據函數單調性化簡方程F(x)=0得n=4x-2x+1+3,再根據二次函數值域求實數n的取值范圍.
試題解析:(1)∵函數f(x)為偶函數,∴f(-x)=f(x),即(-x)·(1-![]() )=x·(1-
)=x·(1-![]() ).
).
∴x·(2-a)=0,由于x不恒為0,∴a=2.3分
故f(x)=x(1-![]() )=x·
)=x·![]() .
.
又x∈[1,2],∴2x-1>0,2x+1>0,
∴不等式m·![]() ≥2x+1恒成立,等價于m≥2x-1恒成立.
≥2x+1恒成立,等價于m≥2x-1恒成立.
又x∈[1,2],∴2x-1∈[1,3],∴當m≥3時,不等式m≥2x-1恒成立,
∴實數m的取值范圍為[3,+∞).
(2)函數F(x)=g(4x-n)-g(2x+1-3)有零點,等價于方程g(4x-n)-g(2x+1-3)=0有實數根.由(1)知f(x)=x(1-![]() ),
),
∴g(x)=1-![]() =
=![]() (x≠0).
(x≠0).
由2x+1是增函數,∴g(x)是減函數.9分
∴4x-n=2x+1-3,
∴n=4x-2x+1+3.
∵4x-2x+1+3
=(2x)2-2·2x+3
=(2x-1)2+2,
又x≠0,∴(2x-1)2+2>2.
故實數n的取值范圍是(2,+∞).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】對于定義域為R的函數f(x),若f(x)在(-∞,0)和(0,+∞)上均有零點,則稱函數f(x)為“含界點函數”,則下列四個函數中,不是“含界點函數”的是( )
A. f(x)=x2+bx-1(b∈R) B. f(x)=2-|x-1|
C. f(x)=2x-x2 D. f(x)=x-sin x
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,如果存在正實數
,如果存在正實數![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為
為![]() 上的“
上的“![]() 的型增函數”,已知
的型增函數”,已知![]() 是定義在
是定義在![]() 上的奇函數,且在
上的奇函數,且在![]() 時,
時, ![]() ,若
,若![]() 為
為![]() 上的“2017的型增函數”,則實數
上的“2017的型增函數”,則實數![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的運動方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
步數 性別 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 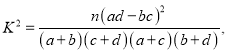
(1)已知某人一天的走路步數超過8000步被系統評定為“積極型”,否則為“懈怠型”,根據題意完成下面的 積極型 懈怠型 總計 男 女 總計 (2)若小王以這40位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選2人,其中每日走路不超過5000步的有![]() 列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?![]() 人,超過10000步的有
人,超過10000步的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 右頂點與右焦點的距離為
右頂點與右焦點的距離為![]() ,短軸長為
,短軸長為![]()
(I)求橢圓的方程;
(Ⅱ)過左焦點F的直線與橢圓分別交于A、B兩點,若三角形OAB的面積為![]() 求直線AB的方程。
求直線AB的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() (其中e是自然對數的底數,常數a>0).
(其中e是自然對數的底數,常數a>0).
(1)當a=1時,求曲線在(0,f(0))處的切線方程;
(2)若存在實數x∈(a,2],使得不等式f(x)≤e2成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
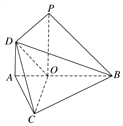
【題目】如圖,在△ABC中,∠ABC=45°,點O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求證:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直線
所在平面于直線![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
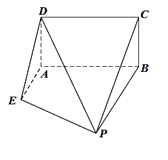
(Ⅰ)設點![]() 為棱
為棱![]() 中點,求證:
中點,求證: ![]() 平面
平面![]() ;
;
(Ⅱ)線段![]() 上是否存在一點
上是否存在一點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,試確定點
?若存在,試確定點![]() 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com