
【題目】已知函數f(x)= ![]() ,是定義在R上的奇函數. (Ⅰ)求函數f(x)的解析式;
,是定義在R上的奇函數. (Ⅰ)求函數f(x)的解析式;
(Ⅱ)求函數f(x)的值域.
【答案】解:(Ⅰ)f(x)在R上的奇函數,f(0)=0,得b=﹣1, ∴f(x)= ![]() ,
,
又∵f(﹣x)=﹣f(x),
∴ ![]() =﹣
=﹣ ![]() ,化簡得,
,化簡得, ![]() =
= ![]() ,
,
∴a=1,∴f(x)= ![]() ;
;
(Ⅱ)f(x)=1﹣ ![]() ,求得:﹣1<f(x)<1,
,求得:﹣1<f(x)<1,
∴函數值域為(﹣1,1)
【解析】(Ⅰ)根據函數的奇偶性求出a,b的值,從而求出f(x)的解析式;(Ⅱ)將f(x)的解析式變形,求出函數f(x)的值域即可.
【考點精析】關于本題考查的函數的值域,需要了解求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知由甲、乙兩位男生和丙、丁兩位女生組成的四人沖關小組,參加由安徽衛視推出的大型戶外競技類活動《男生女生向前沖》.活動共有四關,若四關都闖過,則闖關成功,否則落水失敗.設男生闖過一至四關的概率依次是![]() ,女生闖過一至四關的概率依次是
,女生闖過一至四關的概率依次是![]() .
.
(Ⅰ)求男生甲闖關失敗的概率;
(Ⅱ)設![]() 表示四人沖關小組闖關成功的人數,求隨機變量
表示四人沖關小組闖關成功的人數,求隨機變量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列幾種說法: ①若logablog3a=1,則b=3;
②若a+a﹣1=3,則a﹣a﹣1= ![]() ;
;
③f(x)=log(x+ ![]() 為奇函數;
為奇函數;
④f(x)= ![]() 為定義域內的減函數;
為定義域內的減函數;
⑤若函數y=f(x)是函數y=ax(a>0且a≠1)的反函數,且f(2)=1,則f(x)=log ![]() x,其中說法正確的序號為 .
x,其中說法正確的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(Ⅰ)函數f(x)滿足對任意的實數x,y都有f(xy)=f(x)+f(y),且f(4)=2,求f( ![]() )的值; (Ⅱ)已知函數f(x)是定義在[﹣1,1]上的奇函數,且f(x)在[﹣1,1]上遞增,求不等式f(x+
)的值; (Ⅱ)已知函數f(x)是定義在[﹣1,1]上的奇函數,且f(x)在[﹣1,1]上遞增,求不等式f(x+ ![]() )+f(x﹣1)<0
)+f(x﹣1)<0
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)的圖象是由y=sin2x向右平移 ![]() 得到,則下列結論正確的是( )
得到,則下列結論正確的是( )
A.f(0)<f(2)<f(4)
B.f(2)<f(0)<f(4)
C.f(0)<f(4)<f(2)
D.f(4)<f(2)<f(0)
查看答案和解析>>
科目:高中數學 來源: 題型:
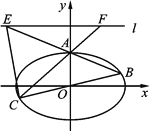
【題目】如圖,在平面直角坐標系![]() 中,橢圓:
中,橢圓: ![]() 的離心率為
的離心率為![]() ,直線l:y=2上的點和橢圓上的點的距離的最小值為1.
,直線l:y=2上的點和橢圓上的點的距離的最小值為1.
(Ⅰ) 求橢圓的方程;
(Ⅱ) 已知橢圓的上頂點為A,點B,C是上的不同于A的兩點,且點B,C關于原點對稱,直線AB,AC分別交直線l于點E,F.記直線![]() 與
與![]() 的斜率分別為
的斜率分別為![]() ,
, ![]() .
.
① 求證: ![]() 為定值;
為定值;
② 求△CEF的面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com