
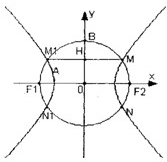
 如圖F1(-c,0),F2(c,0)為雙曲線E的兩焦點,以F1F2為直徑的圓O與雙曲線E交于M、N、M1、N1,B是圓O與y軸的交點,連接MM1與OB交于H,且H是OB的中點.
如圖F1(-c,0),F2(c,0)為雙曲線E的兩焦點,以F1F2為直徑的圓O與雙曲線E交于M、N、M1、N1,B是圓O與y軸的交點,連接MM1與OB交于H,且H是OB的中點.| F1A |
| AM |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
| 2 |
| F1A |
| AM |
| ||
| 2 |
| c |
| 2 |
(
| ||
| 2(1+λ) |
| λc |
| 2(1+λ) |
(
| ||
| 4(1+λ)2a2 |
| λ2c2 |
| 4(1+λ)2b2 |
| 2 |
| c |
| a |
| c |
| b |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
|
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
| 2 |
| 3 |
| 2 |
| F1A |
| AM |
| ||
| 2 |
| c |
| 2 |
(
| ||
| 2(1+λ) |
| λc |
| 2(1+λ) |
(
| ||
| 4(1+λ)2a2 |
| λ2c2 |
| 4(1+λ)2b2 |
| 2 |
| c |
| a |
| c |
| b |
| 2 |
| ||
| 4 |
| ||
| 4 |
| F1A |
| AM |


科目:高中數學 來源: 題型:
 如圖,橢圓C:
如圖,橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| AP |
| PB |
查看答案和解析>>
科目:高中數學 來源:冷水江市一中2007屆高三第十次模擬考試理科數學試卷 題型:044
如圖F1(-c,0)F2(c,0)為雙曲線E的兩焦點,以F1F2為直徑的圓O與雙曲線E交于M、N、M1、N1,B是圓O與y軸的交點,連接MM1與OB交于H,且H是OB的中點,

(1)當c=1時,求雙曲線E的方程;(4分)
(2)試證:對任意的正實數c,雙曲線E的離心率為常數;(4分)
(3)連接F1M與雙曲線E交于點A,是否存在常數![]() 恒成立,若存在試求出λ的值;若不存在,請說明理由.(5分)
恒成立,若存在試求出λ的值;若不存在,請說明理由.(5分)
查看答案和解析>>
科目:高中數學 來源:江蘇省常州高級中學2007~2008學年第三次階段教學質量調研高三數學(文科) 題型:044
如圖F1(-c,0),F2(c,0)為雙曲線E的兩焦點,以F1F2為直徑的圓O與雙曲線E交于M、N、M1、N1,B是圓O與y軸的交點,連接MM1與OB交于H,且H是OB的中點,

(1)當c=1時,求雙曲線E的方程;
(2)試證:對任意的正實數c,雙曲線E的離心率為常數;
(3)連接F1M與雙曲線E交于點A,是否存在常數![]() 恒成立,若存在試求出λ的值;若不存在,請說明理由.
恒成立,若存在試求出λ的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:江蘇省常州高級中學2007~2008學年第三次階段教學質量調研高三數學(理科) 題型:044
如圖F1(-c,0),F2(c,0)為雙曲線E的兩焦點,以F1F2為直徑的圓O與雙曲線E交于M、N、M1、N1,B是圓O與y軸的交點,連接MM1與OB交于H,且H是OB的中點,
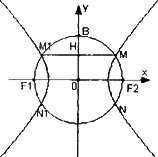
(1)當c=1時,求雙曲線E的方程;
(2)試證:對任意的正實數c,雙曲線E的離心率為常數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com