
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調區間和極值;
的單調區間和極值;
(Ⅱ)求證:當![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 在區間
在區間![]() 上無解.(其中
上無解.(其中![]() )
)
【答案】(Ⅰ)函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,
, ![]() 的單調遞減區間為
的單調遞減區間為![]() .
.![]() 在
在![]() 處取得極大值
處取得極大值![]() ,在
,在![]() 處取得極小值
處取得極小值![]() .
.
(Ⅱ)見解析.
【解析】
試題分析:(Ⅰ)求出導函數![]() ,解方程
,解方程![]() ,列出表格,確定
,列出表格,確定![]() 的符號及
的符號及![]() 的單調性,從而得出極大值和極小值;(Ⅱ)問題實質上就是證明
的單調性,從而得出極大值和極小值;(Ⅱ)問題實質上就是證明![]() 在
在![]() 上的最大值小于或等于1.因此本小題實質就如第(Ⅰ)小題一樣,求
上的最大值小于或等于1.因此本小題實質就如第(Ⅰ)小題一樣,求![]() 在
在![]() 上的最大值即可(要注意函數在閉區間上的最值可能在區間端點處取得).
上的最大值即可(要注意函數在閉區間上的最值可能在區間端點處取得).
試題解析:(Ⅰ)
因為![]() ,
,
所以![]() ,
,
當![]() 時,
時, .
.
令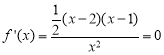 ,得
,得![]() ,
,
所以![]() 隨
隨![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 極大值 |
| 極小值 |
|
所以![]() 在
在![]() 處取得極大值
處取得極大值![]() ,
,
在![]() 處取得極小值
處取得極小值![]() .
.
函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,
,![]() ,
, ![]() 的單調遞減區間為
的單調遞減區間為![]() .
.
(Ⅱ)證明:
不等式![]() 在區間
在區間![]() 上無解,等價于
上無解,等價于![]() 在區間
在區間![]() 上恒成立,
上恒成立,
即函數![]() 在區間
在區間![]() 上的最大值小于等于1.
上的最大值小于等于1.
因為 ,
,
令![]() ,得
,得![]() .
.
因為![]() 時,所以
時,所以![]() .
.
當![]() 時,
時,![]() 對
對![]() 成立,函數
成立,函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
所以函數![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,
,
所以不等式![]() 在區間
在區間![]() 上無解;
上無解;
當![]() 時,
時,![]() 隨
隨![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
| ↘ | 極小值 | ↗ |
所以函數![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() 或
或![]() .
.
此時![]() ,
,![]() ,
,
所以![]()
![]() .
.
綜上,當![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 在區間
在區間![]() 上無解.
上無解.


科目:高中數學 來源: 題型:
【題目】為了解某地區中學生的身體發育狀況,擬采用分層抽樣的方法從甲、乙、丙三所中學抽取![]() 個教學班進行調查.已知甲、乙、丙三所中學分別有
個教學班進行調查.已知甲、乙、丙三所中學分別有![]() ,
, ![]() ,
, ![]() 個教學班.
個教學班.
(Ⅰ)求從甲、乙、丙三所中學中分別抽取的教學班的個數.
(Ⅱ)若從抽取的![]() 個教學班中隨機抽取
個教學班中隨機抽取![]() 個進行調查結果的對比,求這
個進行調查結果的對比,求這![]() 個教學班中至少有一個來自甲學校的概率.
個教學班中至少有一個來自甲學校的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的長軸長為4,離心率為
的長軸長為4,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過右焦點![]() 作一條不與坐標軸平行的直線
作一條不與坐標軸平行的直線![]() ,若
,若![]() 交橢圓
交橢圓![]() 與
與![]() 、
、![]() 兩點,點
兩點,點![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,定點A(-2,0),B(2,0).
,定點A(-2,0),B(2,0).

(1) 若橢圓C上存在點T,使得![]() ,求橢圓C的離心率的取值范圍;
,求橢圓C的離心率的取值范圍;
(2) 已知點![]() 在橢圓C上.
在橢圓C上.
①求橢圓C的方程;
②記M為橢圓C上的動點,直線AM,BM分別與橢圓C交于另一點P,Q,若![]() ,
, ![]() .求λ+μ的值.
.求λ+μ的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com