【題目】已知不等式
的解集為
．
（1）求
的值；
（2）若不等式
的解集為
，不等式
的解集為
，且
，求實數
的取值范圍.
【答案】（1）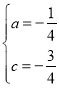
；（2）
.
【解析】
試題分析：（1）利用一元二次不等式的解集與相應的一元二次方程的實數根的關系即可求出；(2)“
”是“
”的充分不必要條件,將它們對應的不等式分別解出,可得集合
從而建立關于
的不等關系,解關于不等式即可得到實數的取值范圍.
試題解析：（1）依題意得，1、3是方程
的兩根，且
，．．．．．．．．．．．．．．．1分
所以，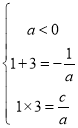
．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 3分
解得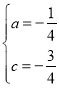；．．．．．．．．．．．．．．．．．．． 5分
（2）由（1）得
，所以，即為
，
解得，
，∴
，
又
，即為解得
，∴
，．．．．．．．．．．．．8分
∵
，∴，
∴
，即
，
∴
的取值范圍是．．．．．．．．．．．．．．．10分
科目：高中數學 來源： 題型：
【題目】某地為制定初中七、八、九年級學生校服的生產計劃，有關部門準備對180名初中男生的身高作調查．
（1）為了達到估計該地初中三個年級男生身高分布的目的，你認為采用怎樣的調查方案比較合理？
（2）表中的數據是使用了某種調查方法獲得的：七、八、九年級180名男生身高：
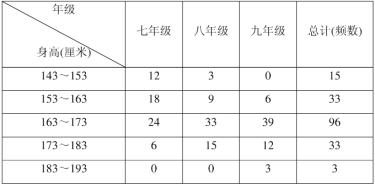
注：表中每組可含最低值，不含最高值．
根據表中的數據，請你給校服生產廠家指定一份生產計劃思路．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，有一段河流，河的一側是以O為圓心，半徑為
米的扇形區域OCD，河的另一側是一段筆直的河岸l，岸邊有一煙囪AB（不計B離河岸的距離），且OB的連線恰好與河岸l垂直，設OB與圓弧
的交點為E．經測量，扇形區域和河岸處于同一水平面，在點C，點O和點E處測得煙囪AB的仰角分別為
，
和
．
（1）求煙囪AB的高度；
（2）如果要在CE間修一條直路，求CE的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系中，以坐標原點為極點，
軸為正半軸建立極坐標系，圓
的極坐標方程為
，直線
的參數方程為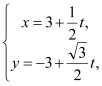
（t為參數）.
（1）求圓的直角坐標方程；
（2）求直線分圓所得的兩弧程度之比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如下圖，已知四棱錐
中，底面
為菱形，
平面
，
，
，
分別是
，
的中點.
（I）證明：
平面
；
（II）取
，在線段
上是否存在點
，使得
與平面
所成最大角的正切值為
，若存在，請求出
點的位置；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某飛機失聯，經衛星偵查，其最后出現在小島
附近，現派出四艘搜救船
，為方便聯絡，船
始終在以小島為圓心，100海里為半徑的圓上，船構成正方形編隊展開搜索，小島在正方形編隊外（如圖）.設小島到
的距離為
，
，
船到小島的距離為
.
（1）請分別求關于
的函數關系式
，并分別寫出定義域；
（2）當兩艘船之間的距離是多少時搜救范圍最大（即最大）？
查看答案和解析>>
科目：高中數學 來源： 題型：
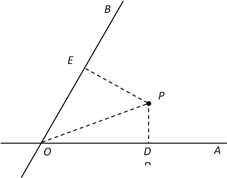
【題目】如圖，
、
是兩條公路（近似看成兩條直線），
，在
內有一紀念塔
（大小忽略不計），已知到直線、的距離分別為
、
，=6千米，=12千米．現經過紀念塔修建一條直線型小路，與兩條公路、分別交于點
、
．
（1）求紀念塔到兩條公路交點
處的距離；
（2）若紀念塔為小路
的中點，求小路的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為增強市民的節能環保意識，鄭州市面向全市征召義務宣傳志愿者，從符合條件的500名志愿者中隨機抽取100名，其年齡頻率分布直方圖如圖所示，其中年齡分組區是：
．
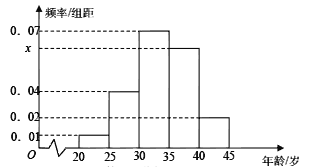
（Ⅰ）求圖中
的值，并根據頻率分布直方圖估計這500名志愿者中年齡在
歲的人數；
（Ⅱ）在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取10名參加中心廣場的宣傳活動，再從這10名志愿者中選取3名擔任主要負責人．記這3名志愿者中“年齡低于35歲”的人數為
，求
的分布列及數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
