【題目】2016年9月，第22屆魯臺經貿洽談會在濰坊魯臺會展中心舉行，在會展期間某展銷商銷售一種商品，根據市場調查，每件商品售價x（元）與銷量t（萬元）之間的函數關系如圖所示，又知供貨價格與銷量呈反比，比例系數為20．（注：每件產品利潤=售價﹣供貨價格）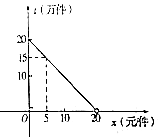 
（1）求售價15元時的銷量及此時的供貨價格；
（2）當銷售價格為多少時總利潤最大，并求出最大利潤．
科目：高中數學 來源： 題型：
【題目】設l，m是兩條不同直線，α是一個平面，則下列四個命題正確的是（ ）
A.若l⊥m，mα，則l⊥α
B.若l∥α，m∥α，則l∥m
C.若l∥α，mα，則l∥m
D.若l⊥α，l∥m，則m⊥α
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體ABCDEF中，四邊形ABCD是正方形，EF∥AB，EF⊥FB，AB=2EF，∠BFC=90°，BF=FC，H為BC的中點．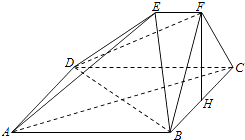
（1）求證：FH∥平面EDB；
（2）求證：AC⊥平面EDB；
（3）解：求二面角B﹣DE﹣C的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）=﹣ 
x3+ 
x2+2ax．
（1）若f（x）在（ 
，+∞）上是單調減函數，求實數a的取值范圍．
（2）當0＜a＜2時，f（x）在[1，4]上的最小值為﹣ 
，求f（x）在該區間的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中，平面
平面
，四邊形
為菱形，點
是棱
上不同于
， 
的點，平面
與棱
交于點
， 
， 
， 
．
（Ⅰ）求證： 
∥平面
；
（Ⅱ）求證： 
平面
；
（Ⅲ）若二面角
為
，求
的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a∈R，函數f（x）═log2（ 
+a）．
（1）若f（1）＜2，求實數a的取值范圍；
（2）設函數g（x）=f（x）﹣log2[（a﹣4）x+2a﹣5]，討論函數g（x）的零點個數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知偶函數f（x）的定義域為R，且在（﹣∞，0）上是增函數，則f（﹣ 
）與f（a2﹣a+1）的大小關系為（ ）
A.f（﹣ ）＜f（a2﹣a+1）
B.f（﹣ ）＞f（a2﹣a+1）??
C.f（﹣ ）≤f（a2﹣a+1）
D.f（﹣ ）≥f（a2﹣a+1）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中點． 
（1）求證：平面CFM⊥平面BDF；
（2）點N在CE上，EC=2，FD=3，當CN為何值時，MN∥平面BEF．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
