
【題目】已知點P(x,y)是平面內的動點,定點F(1,0),定直線l:x=﹣1與x軸交于點E,過點P作PQ⊥l于點Q,且滿足![]()
![]()
![]()
![]()
![]() .
.
(1)求動點P的軌跡t的方程;
(2)過點F作兩條互相垂直的直線,分別交曲線t于點A,B,和點C,D.設線段AB和線段CD的中點分別為M和N,記線段MN的中點為K,點O為坐標原點,求直線OK的斜率k的取值范圍.
【答案】(1)y2=4x;(2)[![]() ,0)∪(0,
,0)∪(0,![]() ].
].
【解析】
(1)利用直接法求軌跡方程,直接通過所給條件![]()
![]()
![]() 列式整理可得y2=4x;
列式整理可得y2=4x;
(2)設直線AB:x=my+1,聯立y2=4x,整理得y2﹣4my﹣4=0,利用韋達定理可得M點坐標(2m2+1,2m),同理可得N點坐標(![]() ,
,![]() ),可得k
),可得k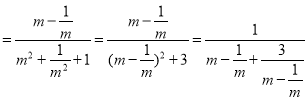 ,整理即可得解.
,整理即可得解.
(1)根據條件可知![]() (x+1,y),
(x+1,y),![]() (2,0),
(2,0),
![]() (x﹣1,y),
(x﹣1,y),![]() (﹣2,y),
(﹣2,y),
因為![]()
![]()
![]() ,
,
所以2x+2=﹣2x+2+y2,即y2=4x,
所以P的軌跡方程為y2=4x;
(2)設直線AB:x=my+1,A(x1,y1),B(x2,y2),
聯立 ,整理得y2﹣4my﹣4=0,且y1+y2=4m,y1y2=﹣4,△=16(m2+1),
,整理得y2﹣4my﹣4=0,且y1+y2=4m,y1y2=﹣4,△=16(m2+1),
所以M(2m2+1,2m),同理,N(![]() ,
,![]() ),所以K(m2
),所以K(m2![]() 1,m
1,m![]() ),
),
所以當k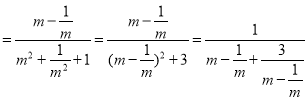 ,
,
令t=m![]() 0,則k
0,則k![]() ,
,
當t<0時,t![]() (﹣t
(﹣t![]() )
)![]() ﹣2
﹣2![]() ,當且僅當t
,當且僅當t![]() 時取等號,
時取等號,
當t![]() 0時,t
0時,t![]() 2
2![]() ,當且僅當t
,當且僅當t![]() 時取等號,
時取等號,
則k![]() ∈[
∈[![]() ,0)∪(0,
,0)∪(0,![]() ].
].


科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,
,![]() ,記
,記![]() ,
,![]() ,若同時滿足條件①
,若同時滿足條件①![]() ,
,![]() 均單調遞增;②
均單調遞增;②![]() 且
且![]() ,則稱
,則稱![]() ,
,![]() 是無窮互補數列.
是無窮互補數列.
(1)若![]() ,
,![]() ,試判斷數列
,試判斷數列![]() ,
,![]() 是否為無窮互補數列,并說明理由;
是否為無窮互補數列,并說明理由;
(2)若![]() ,且
,且![]() ,
,![]() 是無窮互補數列,求數列
是無窮互補數列,求數列![]() 前
前![]() 項的和.
項的和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為抓住經濟發展的契機,調查了解了近幾年廣告投入對銷售收益的影響,在若干銷售地區分別投入4萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示),由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從0開始計數的.
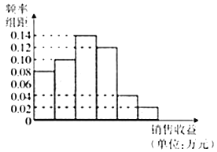
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;并估計該公司分別投入4萬元廣告費用之后,對應地區銷售收益的平均值(以各組的區間中點值代表該組的取值);
(2)該公司按照類似的研究方法,測得另外一些數據,并整理得到如表:
廣告投入x(單位:萬元) | 1 | 2 | 3 | 4 | 5 |
銷售收益y(單位:萬元) | 2 | 3 | 2 | 7 |
由表中的數據顯示,x與y之間存在著線性相關關系,請將(1)的結果填入空白欄,根據表格中數據求出y關于x的回歸真線方程![]() ,并估計該公司下一年投入廣告費多少萬元時,可使得銷售收益達到8萬元?
,并估計該公司下一年投入廣告費多少萬元時,可使得銷售收益達到8萬元?
參考公式:最小二乘法估計分別為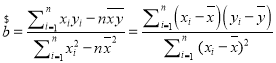 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的方程是![]() ,曲線C的參數方程是
,曲線C的參數方程是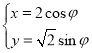 (φ為參數).以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數).以坐標原點O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求直線l和曲線C的極坐標方程;
(2)若![]() 是曲線C上一點,
是曲線C上一點,![]() 是直線l上一點,求
是直線l上一點,求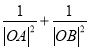 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3﹣(3a﹣2)x2﹣8x+12a+7,g(x)=lnx,記h(x)=min{f(x),g(x)},若h(x)至少有三個零點,則實數a的取值范圍是( )
A.(﹣∞,![]() )B.(
)B.(![]() ,+∞)C.[
,+∞)C.[![]() ,
,![]() )D.[
)D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點.
的中點.
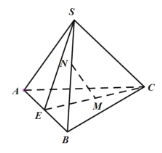
(1)證明:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置并給出證明,若不存在,說明理由;
的位置并給出證明,若不存在,說明理由;
(3)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解戶籍、性別對生育二胎選擇傾向的影響,某地從育齡人群中隨機抽取了容量為200的調查樣本,其中城鎮戶籍與農村戶籍各100人;男性120人,女性80人,繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖,如圖所示,其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
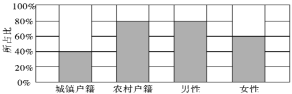
A. 是否傾向選擇生育二胎與戶籍有關
B. 是否傾向選擇生育二胎與性別有關
C. 傾向選擇生育二胎的人群中,男性人數與女性人數相同
D. 傾向選擇不生育二胎的人群中,農村戶籍人數少于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 與
與![]() 滿足的關系;
滿足的關系;
(2)當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(3)當![]() 時,對任意的
時,對任意的![]() ,總有
,總有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線上任意兩點![]()
![]() 處的切線交于點
處的切線交于點![]() ,稱
,稱![]() 為“阿基米德三角形”.當線段
為“阿基米德三角形”.當線段![]() 經過拋物線焦點
經過拋物線焦點![]() 時,
時,![]() 具有以下特征:①
具有以下特征:①![]() 點必在拋物線的準線上;②
點必在拋物線的準線上;②![]() 為直角三角形,且
為直角三角形,且![]() ;③
;③![]() .若經過拋物線
.若經過拋物線![]() 焦點的一條弦為
焦點的一條弦為![]() ,阿基米德三角形為
,阿基米德三角形為![]() ,且點
,且點![]() 的縱坐標為4,則直線
的縱坐標為4,則直線![]() 的方程為( )
的方程為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com