
【題目】設函數![]() ,
,
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)先求函數導數,再根據導數幾何意義得切線斜率為![]() ,最后根據點斜式求切線方程(2)先化簡不等式,并參變分離得
,最后根據點斜式求切線方程(2)先化簡不等式,并參變分離得![]() ,轉化為利用導數求函數
,轉化為利用導數求函數![]() 最小值,利用導數可得
最小值,利用導數可得![]() 單調性,最后利用羅比達法則求最小值
單調性,最后利用羅比達法則求最小值
試題解析:(1)根據題意可得, ![]() ,
,
![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以在點![]() 處的切線方程為
處的切線方程為![]() ,即
,即![]() .
.
(2)根據題意可得, ![]() 在
在![]() 恒成立,
恒成立,
令![]() ,
, ![]() ,
,
所以![]() ,
,
當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 在
在![]() 上是單調遞增,
上是單調遞增,
所以![]() ,
,
所以不等式![]() 成立,即
成立,即![]() 符合題意;
符合題意;
當![]() 時,令
時,令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
當![]() 時,
時, ![]() ,
,
所以![]() 在
在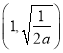 上
上![]() ,在
,在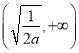 上
上![]() ,
,
所以函數![]() 在
在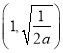 上單調遞增,在
上單調遞增,在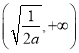 上單調遞減,
上單調遞減,
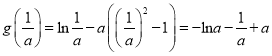 ,令
,令![]() ,
,
![]() 恒成立,又
恒成立,又![]() ,
,
所以![]() ,
,
所以存在![]() ,
,
所以![]() 不符合題意;
不符合題意;
②當![]() 時,
時, ![]()
![]() 在
在![]() 上恒成立,所以函數
上恒成立,所以函數![]() 在
在![]() 上是單調遞減,
上是單調遞減,
所以![]()
顯然![]() 不符合題意;
不符合題意;
綜上所述, ![]() 的取值范圍為
的取值范圍為![]()


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】關于函數 ![]() ,看下面四個結論( ) ①f(x)是奇函數;②當x>2007時,
,看下面四個結論( ) ①f(x)是奇函數;②當x>2007時, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正確結論的個數為:
.其中正確結論的個數為:
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .(x>0)
.(x>0)
(1)函數f(x)在區間(0,+∞)上是增函數還是減函數?證明你的結論;
(2)若當x>0時,f(x)> ![]() 恒成立,求正整數k的最大值.
恒成立,求正整數k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C:x2+y2+4x﹣2y+m=0與直線x﹣ ![]() y+
y+ ![]() ﹣2=0相切.
﹣2=0相切.
(1)求圓C的方程;
(2)若圓C上有兩點M,N關于直線x+2y=0對稱,且|MN|=2 ![]() ,求直線MN的方程.
,求直線MN的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為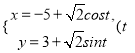 為參數),在以原點
為參數),在以原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立的極坐標系中,直線
軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與
與![]() 軸,
軸, ![]() 軸分別交于
軸分別交于![]() 兩點,點
兩點,點![]() 是圓
是圓![]() 上任一點,求
上任一點,求![]() 兩點的極坐標和
兩點的極坐標和![]() 面積的最小值
面積的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們稱滿足: ![]() (
(![]() )的數列
)的數列![]() 為“
為“![]() 級夢數列”.
級夢數列”.
(1)若![]() 是“
是“![]() 級夢數列”且
級夢數列”且![]() .求:
.求: ![]() 和
和![]() 的值;
的值;
(2)若![]() 是“
是“![]() 級夢數列”且滿足
級夢數列”且滿足![]() ,
, ![]() ,求
,求![]() 的最小值;
的最小值;
(3)若![]() 是“0級夢數列”且
是“0級夢數列”且![]() ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() .證明:
.證明: ![]() (
(![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神十”宇宙飛船進行新產品搭載實驗,計劃搭載若干件新產品A、B,該所要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生的收益來決定具體搭載安排,有關數據如下表:
每件產品A | 每件產品B | ||
研制成本、搭載 | 20 | 30 | 計劃最大資金額 |
產品重量(千克) | 10 | 5 | 最大搭載重量110千克 |
預計收益(萬元) | 80 | 60 |
分別用x,y表示搭載新產品A,B的件數.總收益用Z表示
(1)用x,y列出滿足生產條件的數學關系式,并畫出相應的平面區域; 
(2)問分別搭載新產品A、B各多少件,才能使總預計收益達到最大?并求出此最大收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
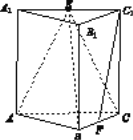
【題目】如圖,在三棱柱ABC A1B1C1中,側棱垂直于底面,AB⊥BC, ![]() ,
,
E,F分別是A1C1,BC的中點.
(Ⅰ)求證:C1F∥平面ABE;
(Ⅱ)求三棱錐E-ABC的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com