
【題目】已知雙曲線![]() ,不與
,不與![]() 軸垂直的直線
軸垂直的直線![]() 與雙曲線右支交于點
與雙曲線右支交于點![]() ,
,![]() ,(
,(![]() 在
在![]() 軸上方,
軸上方,![]() 在
在![]() 軸下方),與雙曲線漸近線交于點
軸下方),與雙曲線漸近線交于點![]() ,
,![]() (
(![]() 在
在![]() 軸上方),
軸上方),![]() 為坐標原點,下列選項中正確的為( )
為坐標原點,下列選項中正確的為( )
A.![]() 恒成立
恒成立
B.若![]() ,則
,則![]()
C.![]() 面積的最小值為1
面積的最小值為1
D.對每一個確定的![]() ,若
,若![]() ,則
,則![]() 的面積為定值
的面積為定值
【答案】ABD
【解析】
對于A選項,設直線![]() 方程為
方程為![]() ,分別與雙曲線方程以及雙曲線的漸近線方程聯立,求出
,分別與雙曲線方程以及雙曲線的漸近線方程聯立,求出![]() 中點坐標,并判斷是否相等即可;對于B選項,由
中點坐標,并判斷是否相等即可;對于B選項,由![]() ,得到
,得到![]() ,結合A選項的結果,即可判斷選項B是否正確;對于C選項,設直線
,結合A選項的結果,即可判斷選項B是否正確;對于C選項,設直線![]() 方程為
方程為![]() ,
,![]() ,直線
,直線![]() 分別與漸近線方程聯立,求出
分別與漸近線方程聯立,求出![]() 坐標,進而求出
坐標,進而求出![]() 的面積,根據
的面積,根據![]() 的范圍,求出
的范圍,求出![]() 的面積的范圍即可;對于D選項,由已知可得
的面積的范圍即可;對于D選項,由已知可得![]() ,利用選項A的方程,得到
,利用選項A的方程,得到![]() 關系,求出
關系,求出![]() 的面積即可.
的面積即可.
設![]() ,代入
,代入![]() 得
得![]() ,①
,①
顯然![]() ,
,![]() ,即
,即![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,![]() 是方程①的兩個根,
是方程①的兩個根,
有![]() ,
,![]() ,
,
設![]() ,
,![]() ,由
,由![]() 得
得![]() ,
,
由![]() ,得
,得![]() ;
;
所以![]() ,所以
,所以![]() 和
和![]() 的中點重合,
的中點重合,
所以![]() ,所以
,所以![]() 恒成立.故A正確.
恒成立.故A正確.
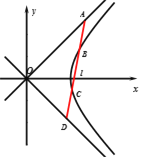
因為![]() 和
和![]() 的中點重合為
的中點重合為![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,故B正確.
,故B正確.
設直線![]() 方程為
方程為![]() ,
,![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,故C錯誤.
,故C錯誤.
因為![]() ,所以
,所以![]() ,得
,得
![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
所以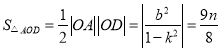 是定值.故D正確.
是定值.故D正確.
故選:ABD.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() 、
、![]() .
.
(1)若![]() ,且函數
,且函數![]() 的圖象是函數
的圖象是函數![]() 圖象的一條切線,求實數
圖象的一條切線,求實數![]() 的值;
的值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若對任意實數![]() ,函數
,函數![]() 在
在![]() 上總有零點,求實數
上總有零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1=0,![]() (n∈N*),前n項和為Sn (參考數據: ln2≈0.693,ln3≈1.099),則下列選項中錯誤的是( )
(n∈N*),前n項和為Sn (參考數據: ln2≈0.693,ln3≈1.099),則下列選項中錯誤的是( )
A.![]() 是單調遞增數列,
是單調遞增數列,![]() 是單調遞減數列B.
是單調遞減數列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某病毒研究所為了更好地研究“新冠”病毒,計劃改建十個實驗室,每個實驗室的改建費用分為裝修費和設備費,每個實驗室的裝修費都一樣,設備費從第一到第十實驗室依次構成等比數列,已知第五實驗室比第二實驗室的改建費用高42萬元,第七實驗室比第四實驗室的改建費用高168萬元,并要求每個實驗室改建費用不能超過1700萬元.則該研究所改建這十個實驗室投入的總費用最多需要( )
A.3233萬元B.4706萬元C.4709萬元D.4808萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() ,且
,且![]() ,現有如下四個結論:
,現有如下四個結論:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱錐
三棱錐![]() 的體積為定值;
的體積為定值;![]() 異面直線
異面直線![]() 所成的角為定值,
所成的角為定值,
其中正確結論的序號是______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,以
,以![]() 為圓心過橢圓左頂點
為圓心過橢圓左頂點![]() 的圓與直線
的圓與直線![]() 相切于
相切于![]() ,且滿足
,且滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,問
,問![]() 內切圓面積是否有最大值?若有,求出最大值;若沒有,說明理由.
內切圓面積是否有最大值?若有,求出最大值;若沒有,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司準備設計一個精美的心形巧克力盒子,它是由半圓![]() 、半圓
、半圓![]() 和正方形ABCD組成的,且
和正方形ABCD組成的,且![]() .設計人員想在心形盒子表面上設計一個矩形的標簽EFGH,標簽的其中兩個頂點E,F在AM上,另外兩個頂點G,H在CN上(M,N分別是AB,CB的中點).設EF的中點為P,
.設計人員想在心形盒子表面上設計一個矩形的標簽EFGH,標簽的其中兩個頂點E,F在AM上,另外兩個頂點G,H在CN上(M,N分別是AB,CB的中點).設EF的中點為P,![]() ,矩形EFGH的面積為
,矩形EFGH的面積為![]() .
.
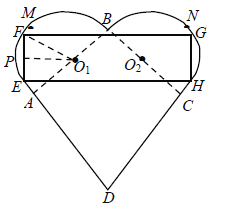
(1)寫出S關于![]() 的函數關系式
的函數關系式![]()
(2)當![]() 為何值時矩形EFGH的面積最大?
為何值時矩形EFGH的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國法定勞動年齡是![]() 周歲至退休年齡(退休年齡一般指男
周歲至退休年齡(退休年齡一般指男![]() 周歲,女干部身份
周歲,女干部身份![]() 周歲,女工人
周歲,女工人![]() 周歲).為更好了解我國勞動年齡人口變化情況,有關專家統計了
周歲).為更好了解我國勞動年齡人口變化情況,有關專家統計了![]() 年我國勞動年齡人口和
年我國勞動年齡人口和![]() 周歲人口數量(含預測),得到下表:
周歲人口數量(含預測),得到下表:
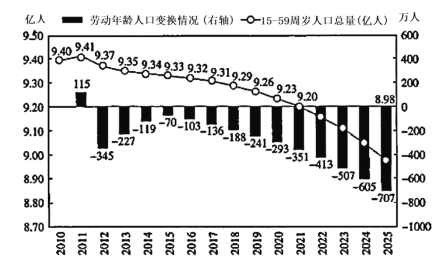
其中![]() 年勞動年齡人口是
年勞動年齡人口是![]() 億人,則下列結論不正確的是( )
億人,則下列結論不正確的是( )
A.![]() 年勞動年齡人口比
年勞動年齡人口比![]() 年減少了
年減少了![]() 萬人以上
萬人以上
B.![]() 這
這![]() 年
年![]() 周歲人口數的平均數是
周歲人口數的平均數是![]() 億
億
C.![]() 年,
年,![]() 周歲人口數每年的減少率都小于同年勞動人口每年的減少率
周歲人口數每年的減少率都小于同年勞動人口每年的減少率
D.![]() 年這
年這![]() 年
年![]() 周歲人口數的方差小于這
周歲人口數的方差小于這![]() 年勞動人口數的方差
年勞動人口數的方差
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com