
已知函數 (
(
 R).
R).
(1)當 時,求函數
時,求函數 的極值;
的極值;
(2)若函數 的圖象與
的圖象與 軸有且只有一個交點,求
軸有且只有一個交點,求 的取值范圍.
的取值范圍.
(1)當 時,
時,  取得極大值為
取得極大值為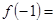
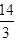 ;
;
當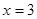 時,
時,  取得極小值為
取得極小值為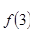
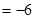 .
.
(2)a的取值范圍是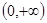 .
.
解析試題分析:(1)遵循“求導數,求駐點,討論駐點兩側導數值符號,確定極值”.
(2)根據 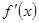 =
= 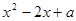 ,得到△=
,得到△= 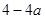 =
= 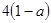 .
.
據此討論:① 若a≥1,則△≤0,
此時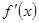 ≥0在R上恒成立,f(x)在R上單調遞增 .
≥0在R上恒成立,f(x)在R上單調遞增 .
計算f(0) ,
,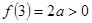 ,得到結論.
,得到結論.
② 若a<1,則△>0,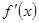 = 0有兩個不相等的實數根,不妨設為
= 0有兩個不相等的實數根,不妨設為 .
.
有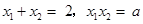 .
.
給出當 變化時,
變化時,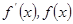 的取值情況表.
的取值情況表.
根據f(x1)·f(x2)>0, 解得a> .作出結論.
.作出結論.
試題解析: (1)當 時,
時,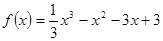 ,
,
∴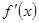
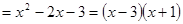 .
.
令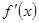 ="0," 得
="0," 得 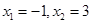 . 2分
. 2分
當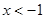 時,
時,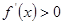 , 則
, 則 在
在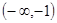 上單調遞增;
上單調遞增;
當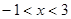 時,
時,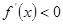 , 則
, 則 在
在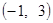 上單調遞減;
上單調遞減;
當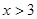 時,
時,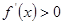 ,
,  在
在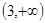 上單調遞增. 4分
上單調遞增. 4分
∴ 當 時,
時,  取得極大值為
取得極大值為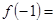
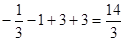 ;
;
當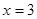 時,
時,  取得極小值為
取得極小值為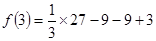
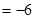 . 6分
. 6分
(2) ∵ 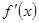 =
= 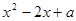 ,
,
∴△= 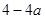 =
= 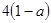 .
.
① 若a≥1,則△≤0, 7分
∴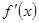 ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上單調遞增 .
∵f(0) ,
,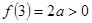 ,
,
∴當a≥1時,函數f(x)的圖象與x軸有且只有一個交點. 9分
② 若a<1,則△>0,
∴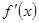 = 0有兩個不相等的實數根,不妨設為
= 0有兩個不相等的實數根,不妨設為 .
.
∴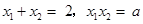 .
.
當 變化時,
變化時,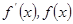 的取值情況如下表:
的取值情況如下表: