
【題目】如圖在四棱錐![]() 中底面
中底面![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,側面
,側面![]() 為正三角形且平面
為正三角形且平面![]() 底面
底面![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點.
的中點.
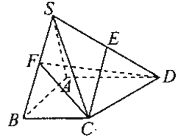
(1)證明:![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)首先取![]() 中點
中點![]() ,連接
,連接![]() ,再證明平面
,再證明平面![]() 平面
平面![]() ,根據面面平行的性質即可證明
,根據面面平行的性質即可證明![]() 平面
平面![]() .
.
(2)首先取![]() 中點
中點![]() ,連接
,連接![]() ,根據平面
,根據平面![]() 底面
底面![]() 得到
得到![]() 底面
底面![]() ,以
,以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,再利用空間向量計算
軸建立空間直角坐標系,再利用空間向量計算![]() 與平面
與平面![]() 所成角即可.
所成角即可.
(1)如圖所示:
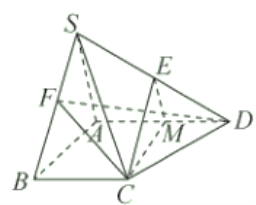
取![]() 中點
中點![]() ,連接
,連接![]() ,
,
因為![]() 為
為![]() 中位線,
中位線,
所以![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() ,
,
又因為![]() ,所以
,所以![]() .
.
所以四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 中點
中點![]() ,連接
,連接![]() .
.
因為![]() ,所以
,所以![]() .
.
因為平面![]() 底面
底面![]() ,
,![]()
所以![]() 底面
底面![]() .
.
以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
如圖所示:
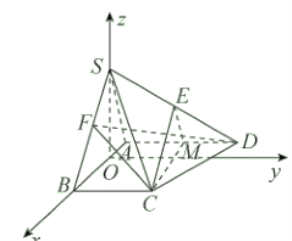
設![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則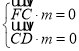 ,即
,即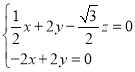 ,
,
可取![]() ,解得
,解得![]() ,
,![]() .
.
則![]() ,
,
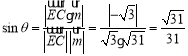 .
.


科目:高中數學 來源: 題型:
【題目】已知正項數列![]() ,
,![]() 滿足:對任意正整數
滿足:對任意正整數![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,![]() ,
,![]() ,
,![]() 成等比數列,且
成等比數列,且![]() ,
,![]() .
.
(Ⅰ)求證:數列![]() 是等差數列;
是等差數列;
(Ⅱ)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(Ⅲ)設![]() =
=![]() +
+![]() +…+
+…+![]() ,如果對任意的正整數
,如果對任意的正整數![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
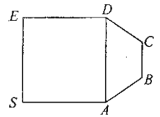
【題目】某產品的包裝紙可類比如圖所示的平面圖形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包裝的過程中,沿著
,在包裝的過程中,沿著![]() 將正方形
將正方形![]() 折起,直至
折起,直至![]() ,得到多面體
,得到多面體![]() ,
,![]() 分別為
分別為![]() 中點.
中點.
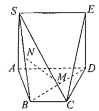
(1)證明:![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為抗擊新冠疫情,某企業組織員工進行用款捐物的愛心活動.原則上每人以自愿為基礎,捐款不超過400元.現項目負責人統計全體員工數據后,下表為隨機抽取的10名員工.的捐款數額.
員工編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
捐款數額 | 124 | 86 | 215 | 53 | 132 | 195 | 400 | 90 | 300 | 225 |
(1)若從這10名員工中任意選取3人,記選到的3人中捐款數額大于200元的人數為X,求X的分布列和數學期望:
(2)以表中選取的10人作為樣本.估計該企業全體員工的捐款情況,現從企業員工中依次抽取8人,若抽到k人的捐款數額小于200元的可能性最大,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com