
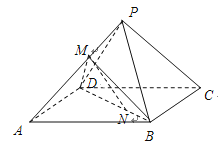
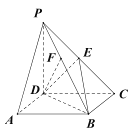
【題目】如圖,在正四棱錐![]() 中,
中,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,
上,![]() .
.
(1)若![]() ,求證:
,求證:![]() ⊥
⊥![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求線段
,求線段![]() 的長.
的長.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題由于圖形是正四棱錐,因此設AC、BD交點為O,則以OA為x軸正方向,以OB為y軸正方向,OP為z軸正方向建立空間直角坐標系,可用空間向量法解決問題.(1)只要證明![]() =0即可證明垂直;(2)設
=0即可證明垂直;(2)設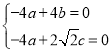 =λ
=λ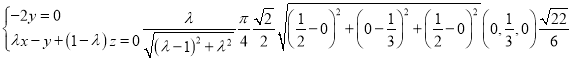 ,得M(λ,0,1-λ),然后求出平面MBD的法向量
,得M(λ,0,1-λ),然后求出平面MBD的法向量![]() ,而平面ABD的法向量為
,而平面ABD的法向量為![]() ,利用法向量夾角與二面角相等或互補可求得
,利用法向量夾角與二面角相等或互補可求得![]() .
.
試題解析: (1)連結AC、BD交于點O,以OA為x軸正方向,以OB為y軸正方向,OP為z軸正方向建立空間直角坐標系.
因為PA=AB=![]() ,
,
則A(1,0,0),B(0,1,0),D(0,-1,0),P(0,0,1).
由![]() =
=![]() ,得N
,得N![]() ,
,
由![]() =
=![]() ,得M
,得M![]() ,
,
所以![]() ,
,![]() =(-1,-1,0).
=(-1,-1,0).
因為![]() =0,所以MN⊥AD
=0,所以MN⊥AD
(2) 解:因為M在PA上,可設![]() =λ
=λ![]() ,得M(λ,0,1-λ).
,得M(λ,0,1-λ).
所以![]() =(λ,-1,1-λ),
=(λ,-1,1-λ),![]() =(0,-2,0).
=(0,-2,0).
設平面MBD的法向量![]() =(x,y,z),
=(x,y,z),
由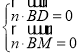 ,得
,得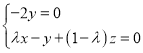
其中一組解為x=λ-1,y=0,z=λ,所以可取![]() =(λ-1,0,λ).
=(λ-1,0,λ).
因為平面ABD的法向量為![]() =(0,0,1),
=(0,0,1),
所以cos![]() =
=![]() ,即
,即![]() =
=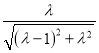 ,解得λ=
,解得λ=![]() ,
,
從而M![]() ,N
,N![]() ,
,
所以MN=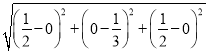 =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() =1(a>0,b>0)的一條漸近線方程為2x+y=0,且頂點到漸近線的距離為
=1(a>0,b>0)的一條漸近線方程為2x+y=0,且頂點到漸近線的距離為![]() .
.
(1)求此雙曲線的方程;
(2)設P為雙曲線上一點,A,B兩點在雙曲線的漸近線上,且分別位于第一、二象限,若![]() ,求△AOB的面積.
,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解戶籍、性別對生育二胎選擇傾向的影響,某地從育齡人群中隨機抽取了容量為200的調查樣本,其中城鎮戶籍與農村戶籍各100人;男性120人,女性80人,繪制不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例圖,如圖所示,其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述中錯誤的是( )
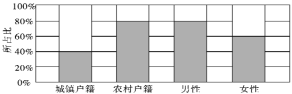
A. 是否傾向選擇生育二胎與戶籍有關
B. 是否傾向選擇生育二胎與性別有關
C. 傾向選擇生育二胎的人群中,男性人數與女性人數相同
D. 傾向選擇不生育二胎的人群中,農村戶籍人數少于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() 平面
平面![]() ,
,![]() 是棱
是棱![]() 上的一點,滿足
上的一點,滿足![]() 平面
平面![]() .
.
(Ⅰ)證明:![]() ;
;
(Ⅱ)設![]() ,
,![]() ,若
,若![]() 為棱
為棱![]() 上一點,使得直線
上一點,使得直線![]() 與平面
與平面![]() 所成角的大小為30°,求
所成角的大小為30°,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心為
的圓心為![]() ,直線l過點
,直線l過點![]() 且與x軸不重合,l交圓
且與x軸不重合,l交圓![]() 于C,D兩點,過
于C,D兩點,過![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點E.設點E的軌跡為
于點E.設點E的軌跡為![]() .
.
(1)求![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 相切于點M,
相切于點M,![]() 與兩坐標軸的交點為A與B,直線
與兩坐標軸的交點為A與B,直線![]() 經過點M且與
經過點M且與![]() 垂直,
垂直,![]() 與
與![]() 的另一個交點為N,當
的另一個交點為N,當![]() 取得最小值時,求
取得最小值時,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若![]() 的值域為
的值域為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在這祥的實數
,是否存在這祥的實數![]() ,使函數
,使函數![]() 在區間
在區間![]() 內有且只有一個零點.若存在,求出
內有且只有一個零點.若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,其前
,其前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求證:數列
),求證:數列![]() 是等比數列;
是等比數列;
⑵若數列![]() 是等比數列,求
是等比數列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求證:數列
,求證:數列![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】衡陽市八中對參加“社會實踐活動”的全體志愿者進行學分考核,因該批志愿者表現良好,學校決定考核只有合格和優秀兩個等次.若某志愿者考核為合格,授予1個學分;考核為優秀,授予2個學分,假設該校志愿者甲、乙、丙考核為優秀的概率分別為![]() 、
、![]() 、
、![]() ,他們考核所得的等次相互獨立.
,他們考核所得的等次相互獨立.
(1)求在這次考核中,志愿者甲、乙、丙三人中至少有一名考核為優秀的概率;
(2)記在這次考核中甲、乙、丙三名志愿者所得學分之和為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com